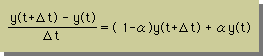
■まとめ■
ここで紹介した3つの方法は、下式のαの値を変えることで表すことができます。そして、各方法のα値と解析精度を、下表にまとめてみました。
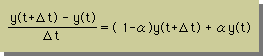
| Method | α | 数値解析の精度 y(t+Δt)/y(t) |
|---|---|---|
| Exact | y(t+Δt)/y(t) = 1 + Δt + (1/2)Δt2 + (1/6)Δt3 + ...... | |
| Explicit | 1 | y(t+Δt)/y(t) = 1 + Δt |
| Implicit | 0 | y(t+Δt)/y(t) = 1 + Δt + Δt2 + ........ |
| Crank-Nicolson | 1/2 | y(t+Δt)/y(t) = 1 + Δt + (1/2)Δt2 + (1/4)Δt3 ....... |
■各方法の安定性■
各方法の計算精度が理解できたところで、今度は各方法の安定性を調べてみることにします。安定性が良いということは、様々な値を時間ステップ(Δt)に使っても、厳密解からさほど遠くない近似解が得られることを言います。
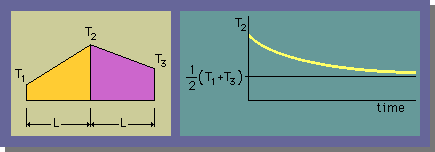
安定性を調べるために、下の左図に示す2要素で分割した領域を考慮します。節点1と3の温度は、Dirichlet型境界条件で与えることにします。よって、未知数は、T2になり、下の右図の様な温度変化を示すはずである。定常解は、T2=(1/2)*(T1+T3)ですね。
| BACK | NEXT |
|---|
| Menu | Heat Equation | Time derivative | Upwind | 1 Dim Example |