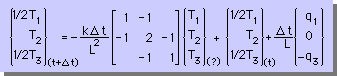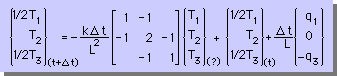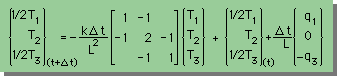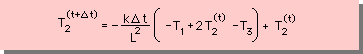Time Derivative

Time Derivative and Upwind Method
Time Derivative Term-6

すると、この場合、次の連立方程式が導かれます。下式の中に(?)が付いている項がありますね。これは、この式を導いた時点では、この項の時刻をまだ決められませんね。つまり、ここに Explicit、Implicit 、Crank-Nicolson　method で定められた時刻が入るわけですよ。

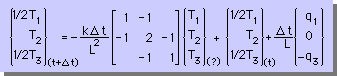
■Explicit method の安定性■
まず、上の連立方程式をExplicit method用にアレンジすると、下式の様になります。つまり、(?)=(t)ですね。

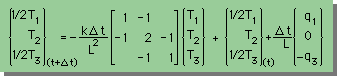これを、T₂について解くと、下式の様になります。 T₁とT₃は、Dirichlet型境界条件で与えられていますので、ベクトル{q}は不要になりますね。

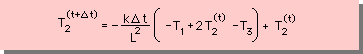上式をちょっとアレンジすると、次の様になります。

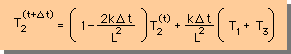この式のΔtに、無限大に近い大きな数値を入れたらどうなるか、考えてみて下さい。結果は明らかですね。つまり、T₂ = 負の無限大になってしまいます。これでは、だめです。したがって、Explicit method を使う場合には、下の条件を満足していることを確認してから使って下さい。

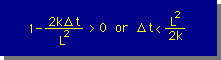実際に数値がおかしくなることを、のちほど例題の計算のところで披露します。