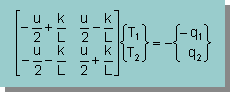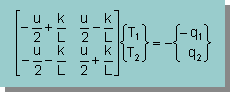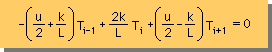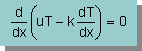また、1つのマトリックスにまとめると、下の様になりますね。

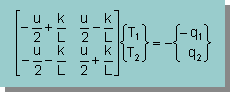もっと分かり易くするために、領域を要素長さ(L)で5等分した時の Global matrix 型の連立方程式を下に示します。

次に、Global matrix 型の連立方程式の中程の式を1行抜いて、一般式を書いてみましょう。 下式の様になりますね。

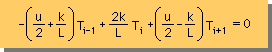この式は、差分法で導いた式と、まったく同じになります。つまり、有限要素法を使わなくても、 簡単に上式にたどり着くことができます。

■一服■
次からは、話題が、がらっと変りますので、ここらへんで一服して下さい。一服しながら でよいですので、次の内容を読んで下さい。
ここで解こうとしている微分方程式ですが、du/dx=0 だから、次の様にも書けますよね。

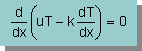しかし、上式の様に書いてしまうと、du/dxがゼロかどうかは、分からなくなってしまいます (ここでは、u を密度流としましょう)。 ただ、数値計算をするときに、一定な u を使うと、du/dx=0 になります。ところが、1次元 の場合、du/dx がゼロでないと言うことは、領域の途中から密度流が 出入りしていることを意味しますよね。と言うことは、1次元の微分方程式(上式)には、領域の境界から密度流の出入りを表す生成項がなくてはならないことになります。しかし、上の式には、それが有りませんね。