| Ti = D1+D2(B/A)i |
ここに、i は整数、D1とD2は境界条件によって決まる定数です。 この時点で明らかなことは、A≠0 です。しかし、よく観察すると A>0 の条件が必要になってきます。 何故かと言うと、A <0だった場合、(B/A)iの値のB/Aの符号が整数iによってスイッチすることになりますね。
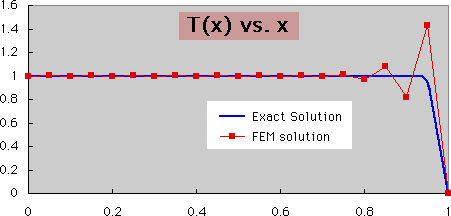
また、|B|>|A| ですから、|(B/A)i| は、iが大きくなりにつれ急激に大きくなります。 ちなみに、下の条件で計算を行うと、下図のグラフ(FEM solution)に示す様な山切りの解が得られます。
| k | u | T(x=0) | T(x=1) | 領域の長さ | 要素数 | 要素の長さ |
|---|---|---|---|---|---|---|
| 1 | 100 | 1 | 0 | 1 | 20 | 0.05 |

図のグラフの様な結果を出す数値計算方法では、解析に役立ちません。 このままで、一応満足する解をだすには、 A>0 にする必要があります。 つまり、要素の長さ(L)を、下式の条件に満足するように、 維持しなければなりません。
| L<2k/u |
これは大変なことです。何故かと言うと、kとuか変わるたびに 要素の長さを変更しなければならないからです。
■Upwind Method■
要素の長さを変更しなくても、理屈にかなった解が得られないかと考え出されたのが、風上差分(後程説明)です。安定した解は得られる様になりましたが、風上差分の解析精度の保証がいまいちでした。
そこで、考えだされたのが、次に示すUpwind Methodです。
| A = 1 - γ + αγ |
| B = 1 + γ + αγ |