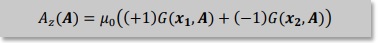
■電流を導線の中心に集中させた場合の考察■
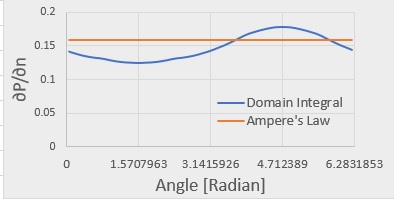
これまでの計算では、1[A]の電流が導線に等しく分布して流れる場合を仮定してインダクタンスを計算してきました。
このような仮定をすると計算式が複雑になり結果を得るのに境界要素法による数値計算が必要になります。
ここでちょっと視点を変えて、電流が導線の中心に集中していたと仮定したらどうなるか考えてみます。
無限遠でAz(∞)=0, B(∞)=0ですので境界要素法を用いると以下の領域積分が残りました。
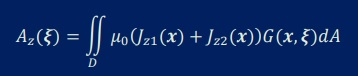
電流を導線の中心に集中させると上の式は、どうなるか考えてみます。その前に以下の図を見て下さい。 赤と緑の点が電流を集中させた位置です。赤色が+1[A]、緑が-1[A]です。
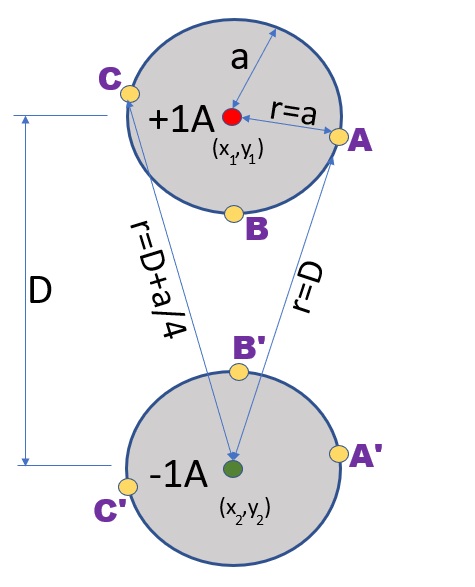
導線の断面の半径は、aです。導線の中心間の距離はDです。 点ξ=Aは2つ導線の中心までの距離がそれぞれaとDの位置です。 点Bは上の導線の最下部です。 この状況を踏まえ上の積分式を点Aで展開すると以下に成ります。