Electromagnetics and Ham Radio
Offcenterfeddp 16

■アンテナ上の座標z=0～λ/4の範囲で給電点を移動させる実験■
ダイポールアンテナの全長を変えずに、左右のエレメント長を変えて入力インピーダンスを測定する試みを幾つか実施しました。最初に試したのが10m長さのスチール製巻き尺を2個使ってアンテナをつくりました。次が極細のスチールワイヤー、その次が断面の直径が2mm位の銅の撚線で、最後が直径12mm長さ1mのアルミパイプを連結してアンテナにしました。今回はアルミパイプでの実験を紹介します。 アンテナと測定器(AA-600)の間に50Ω対200Ωの電流型バランを挿入して実験してみましたが、アンテナの入力インピーダンスの特定が難しく断念しました。 ということで今回は測定器とアンテナの給電点には長さ約200mmの5D-2Vの同軸ケーブルを挿入して実験を試みました。同軸ケーブルには７個のトロイダルコアを通過させコモンモード電流を抑制してあります。 伝送線路方程式によると、アンテナの入力インピーダンス(ZL)、測定器でのインピーダンス(Zin)と同軸ケーブルのインピーダンス(Z0)と長さ(d)の関係は減衰を無視すると、以下の２つの関係式が成り立ちます。ここにβ=2π/λ。

(1)ZLからZinを求める式

\begin{eqnarray} Z_{in}=Z_0\frac{Z_L+jZ_0tan(\beta d)}{Z_0+jZ_Ltan(\beta d)} \end{eqnarray}

(2)ZinからZLを求める式

\begin{eqnarray} Z_L=Z_0\frac{Z_{in}-jZ_0tan(\beta d)}{Z_0-jZ_{in}tan(\beta d)} \end{eqnarray}

また上の最初の式の右辺を操作すると以下の様に書くことが出来ます。

\begin{eqnarray} {Z_LZ}_{in}={Z_0}^2\frac{\frac{Z_L}{Z_0}+jtan(\beta d)}{\frac{Z_0}{Z_L}+jtan(\beta d)} \end{eqnarray}

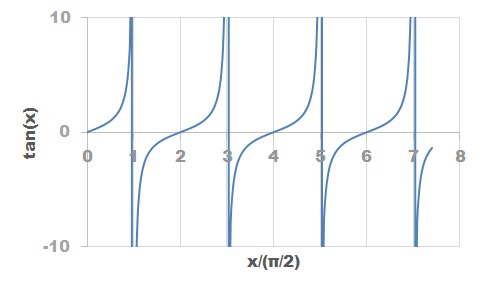
そしてβd=nπ/2, n=1,3,5,…でtan(βd)=∞になります。下図を参考にして下さい。

つまり、d=nλ/4と置くと以下の式が成立します。

\begin{eqnarray} Z_LZ_{in}={Z_0}^2 \end{eqnarray}

この式はスタックアンテナのフィーダー分配に使われるQマッチの式として有名です。

Preceding Page Next Page
Menu Inductance Capacitance Exp Z0 Coaxial Balun Dielectric Off-Center-fed DP Helmholtz FEM BEM
Internet College of Finite Element Method
JR2XSO