2次要素で領域の境界を分割すると、節点の数は、要素の数の2倍になります。ちなみに、1次要素の場合は、節点の数＝要素の数でした。

離散化を続けましょう。前の式を、もう少し詳しく書くと、下の様になります。式を見ると、要素毎に、6つの独立した積分があることに気付くと思います。

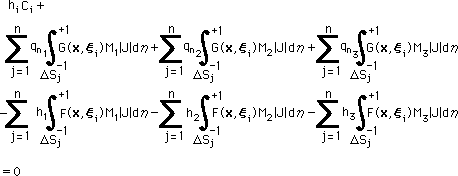
そして、Free term C(ξ) は、F(x,ξ) の積分ですから、下式で計算できます。1次要素のFree term の計算方法も参考にして下さい。

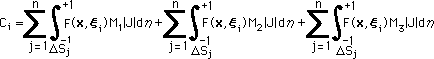
上の2つの式を見た感じ、数値積分は、さほど難しいところは、有りません。ただ、Source point が要素に含まれる場合のG(x,ξ) の積分については、多少注意が必要です。特に、要素が直線でなく、要素上の節点(両端の節点でない) が要素の中央にない場合は、厳密解を得ることが出来ません。

また、F(x,ξ) の積分についても、多少の前準備が必要です。