■注意を要する積分■
実際の数値積分については、1j次要素の積分を参考にして下さい。ここでは、6つの積分のなかから、2つ選んで、数値積分方法を説明することにします。他の4つについては、形状関数を差し替えれば、積分を行うことが出来ます。

最初は、F(x,ξ) に関する積分の方法を説明します。まず、F(x,ξ) とは、何だったか、思い出してみましょう。Index 表示とVector 表示法を用いると、次の様に書くことができました。

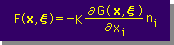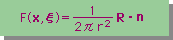復習になりますが、n(s) ＝(dy/ds)i-(dx/ds)j です。そして、ds=|J|dη で表せられます。さらに、dx とdy は、下式によって書くことが出来ました。

すると、unit normal vector (n) は、下式で書き表すことが出来ます。

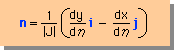
以上のことをまとめると、F(x,ξ) は、次の様になります。

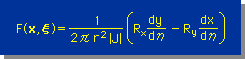
ここに、R_x=x-ξ_x、R_y=y-ξ_y、 dx/dη=ηδ²x+δx、dy/dη=ηδ²y+δy です。