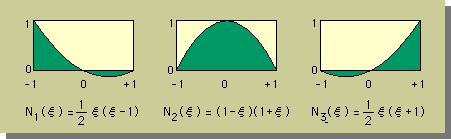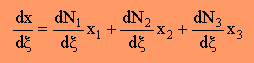coordinatetrans

Calculus in Finite Element Method
Coordinate Transformation-2

■2次の変換式■
線形(1次)では、x₂ が、x₁とx₃ の中央に位置していました。では、x₂ が、その中央にない場合は、どうなるかです。つまり、下図の様な変換の場合ですね。

すると、線形の時と同様に、下の式が成り立ちます。

x = N₁(ξ)x₁ + N₂(ξ)x₂ + N₃(ξ)x₃

そこで気になるのが、N₁, N₂, N₃ は、どんな関数なの？です。答えを言ってしまうと、下図の様になります。形状関数の条件式を満足しているかどうか、チェックしてみて下さい。

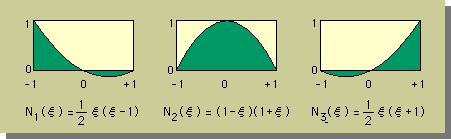そして、dx=(dx/dξ)dξ ですから、dx/dξは、次の様に計算できますね。

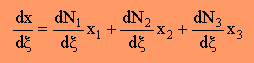これで、2次の変換式を使った積分が出来る様になりましたね。1次元の座標変換は、これぐらいにしておきましょう。 2次元については、2次元パラメトリック要素のところで紹介します。