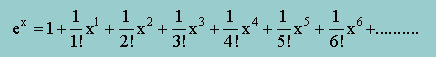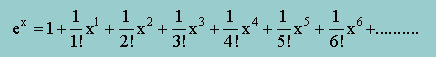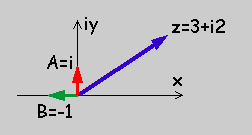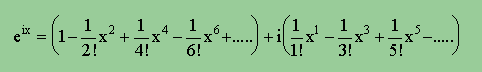Calculus in Finite Element Method
Functions
■ex■
この関数は、exp(x)とも書きます。引数の x に1を代入すると、
2.718281828459 となり、e の値になりますね。そして、ex は、線形1階常微分方程式(dy/dx=y)の解でもありますね。”そう言えば習ったことがある”と言う方も多いと思います。
ここまでは、いいですね。ところで、マクローリン展開とかTaylor series といったものを知っていますか？。関数を x のべき乗の足し算で表す方法です。ex は、次の様になります。
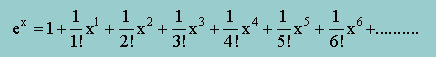ここに、!は、階乗を意味します。4!=4X3X2X1 です。そして、ex は、何回微分しても ex ですよね。上の式の右辺を微分してみて下さい。すると、元の式なりますね。
次に引数の x が複素数だったらどうでしょう。つまり、ez と置き、z=x+iy とします。ここに、ii=-1 です。xを実部、iyを虚部と言い、xとyは、実数です。複素数は、2次元のベクトルだと思って下さい。下に例題を示します。ただ、複素数では、掛け算のルールがベクトルのそれ(2つ有る)と異なります。
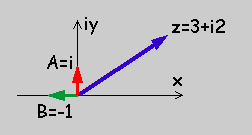例えば、上図の A=i という複素数が有ったとします。それに、同じ複素数 A を掛けたらどうなるでしょう。ii=-1 ですから、AA=-1 ですね。上図の B=-1 がそうです。つまり、ベクトル A が 90度 反時計方向に回転したことになります。つまり、複素数では、ベクトルに i を掛けると、そのベクトルは、90度回転します。
さて、話を前にもどし、ez について考えてみましょう。話を簡単にするために、eix を試してみましょう。ii=-1 に注意して計算すると、次の様になりますね。
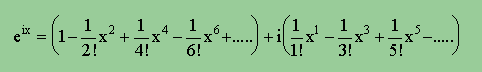上の式を見ると、実部が偶関数(指数が偶数)で、虚部が奇関数になっていますね。上の式を見て、”あれー”と声を上げる人がいると思います。そうです、上の式は、下に示す様に、sin(x)とcos(x) なのです。そして、下の式をDe Moivreの定理と言います。
この定理の副産物に三角関数の式があります。例えば、sin(2x) = 2sin(x)cos(x)が有ります。これは、次の様にして導くことが出来ます。まず、eixeix = ei2x =
cos(2x)+isin(2x)ですよね。確認してみて下さい。さらに、この式は、eixeix = (cos(x)+isin(x))(cos(x)+isin(x)) とも書けますよね。
展開すると、eixeix = (cos2(x)-sin2(x))+i2cos(x)sin(x)
と書けますね。そして、この式とcos(2x)+isin(2x)を実部と実部そして虚部と虚部を照らし合わせると、次の2つのIdentitiesが生まれます。
|
cos(2x) = cos2(x)-sin2(x) |
sin(2x) = 2cos(x)sin(x) |
関数については、この程度の理解があれば、FEMの勉強には差し支え有りません。
ところで、ez = ex
(cos(y)+isin(y)) になりますね。
Menu
NEXT-->Derivative
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)
|