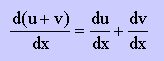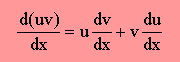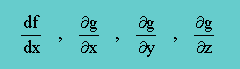
■ d と ∂■
微分方程式の微分を表す記号に、d と ∂ が有ります。d を全微分、∂ を偏微分を表す記号です。微分方程式の未知数(unknown or independent variable)が、1つの従属変数(dependent variable)の関数である場合、例えば f(x) 、微分方程式には、全微分記号(d)が使われます。従属変数とは、座標軸を表す変数(x, y, z)のことです。しかし、微分方程式の未知数が、2つ以上の従属変数で表されている場合、例えば、g(x,y,z)、微分方程式には、偏微分記号(∂)が使われます。関数f(x)は、xのみでしか微分できませんが、関数g(x,y,z)は、x以外に、y と z でも微分出来ますよね。だから、∂ を使うんです。微分の一例を下に示します。

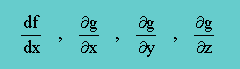
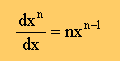
■微分と構成式■
弾性解析の応力(stress)や熱解析の熱流束(heat flux)は、変位や温度の変化率、つまり微分で書かれています。確かに、温度分布に変化が有るから熱は移動し、変位が場所的に変化しているからひずみが生じ応力が発生することになりますね。最初から、ちょっと難しくなってしまいましたが、まー、工学で基本となる法則は、微分の形で書かれていることを理解して頂ければOKです。参考までに、下に熱流束 と弾性解析のひずみの式を示します。眺める程度にしておいて下さいね。あまり深く考えないで下さいね。

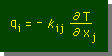
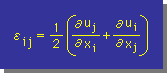
■2つの関数の微分■
関数 u(x) と v(x) があったとします。各々を微分すると、du/dx, dv/dx になりますね。u(x) と v(x) は、x のみの関数ですから、全微分が使われていますね。では、2つの関数の和 u(x)+v(x) の微分は、どうなるでしょうか。下の様になります。