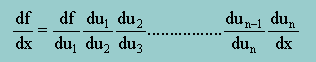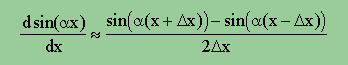
■簡単な関数をxで微分■
微分の作業をやっているとき、なにげなく使っているのが、Chain rule です。
例えば、sin(αx) を x で微分することを考えてみましょう。
結果は、αcos(αx) ですね。信じられない人は、この結果を下の差分で確認してみて下さい。
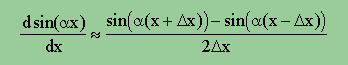
では、sin(αx) からどの様な過程を経て、αcos(αx) が得られたかを考えてみましょう。
まず、sin(αx) は、直接 x で微分出来ませんので、u=αx と置きます。
すると、sin(u) となりますから、u で簡単に微分できますね。答えは、cos(u) です。
また、u は、x で簡単に微分できます。言うまでも有りませんが、答えは、α ですね。
すると、sin(αx) の x での微分は、αとcos(u) の積で得られます。まー、こんな風に教わったと思います。
上の事柄を、f=sin(αx), u=αx とおいて、まとめると、次の様になります。
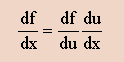
■複雑な関数をxで微分■
上で説明した手順で、微分を行う方法を Chain rule と言います。もーちょと、複雑な関数を取り上げてみましょう。例えば、f=sin(eαx) を x で微分してみます。この場合、f=sin(u), u=ev, v=αx の様におきます。すると、df/dx は、次の様になる。
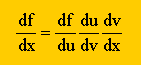
上で説明した事柄を延長すると、Chain rule として、以下の様にまとめることができますね。 ここでやっていることは、簡単な微分ですから、いつでも、差分で Chain rule の結果をチェックできます。