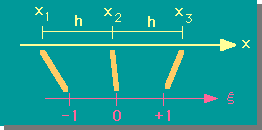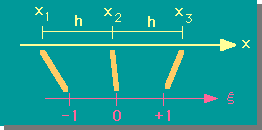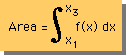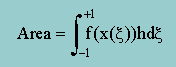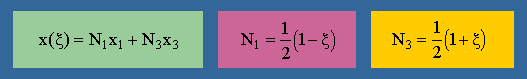coordinatetrans

Calculus in Finite Element Method
Coordinate Transformation

■一番簡単な座標変換■
有限要素法の積分式を数値積分するのに、Gauss-Legendre 法が使われます。そして、その法を使える様にするためには、座標変換が必要になってきます。なぜかと言うと、Gauss-Legendre 法の積分範囲が -1 から +1 の無次元座標になっているからです。ですから、有限要素法を勉強する前に、座標変換をマスターしておく必要があります。 ”私は座標変換を使わずに有限要素法のプログラムをつくりましたよ”と言う人もいるはずです。それは、積分が簡単にできる要素を使っているからです。例えば、1次元の1次要素や2次元3角形要素がそれに値します。

では、手始めに1次元の線形座標変換をやってみましょう。まず、下の図を見て下さい。

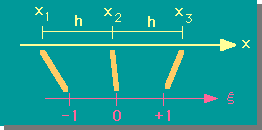上図の x が実座標で、ξ が無次元座標です。では、これら2つの座標軸を関係付ける式がどんな形をしているのでしょう。まー、普通に考えると、下式が浮かんできかすよね。

すると、dx=hdξ と書けかすね。つまり、ξが 1 変化すると、x は、h 増加することになることを意味しています。

次に、この座標変換がどんな風に積分で役立つかを説明しておきましょう。下式の様に、関数 f(x) を積分することを考えます。

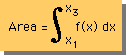上の式の x に座標変換を施すと、次の様になります。

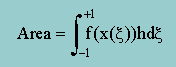何が良いかと言うと、x₁ や x₃ が、どんな値になろうと、関数 f(x) の積分区間を -1 から +1 に固定することができます。便利ですよね。特に、数値積分をするときに、大いに助かります。

ところで先程の座標変換の式ですが、山勘ではなく、システマティックに書けないもんでしょうか。これに応えてくれるのが、要素の形状関数です。ここでは、詳しく述べませんが、変換式は、次の様に書けます。

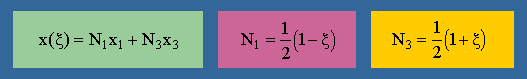式中の N₁ と N₃ は、線形要素の形状関数です。貴方は、上の式と x(ξ)=hξ+x₂ が同じであることを確認して下さいね。 1つ注意を払ってもらいたい事は、N₁(-1)=1, N₁(+1)=0, N₃(+1)=1, N₃(-1)=0 になっていることです。そして、N₁+N₃=1 for all ξ になっていることも確認して下さいね。これらは、形状関数の条件式です。

Ordinary Differential Equations NEXT

Menu Fnc Drv Int(1) Dif Crd Chain Lhsptl Vec Green IndxN Int(2)