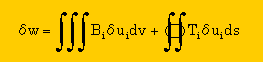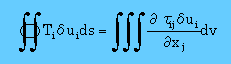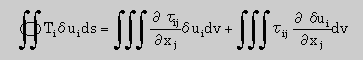Calculus in Finite Element Method
Integration By Parts (2dim & 3dim)-2
部分積分法をより一般的な形で書くと、次の様になります。ちょっと難しい形になっていますね。
まー、この式は、見なかったことにして下さい。

■Solid Mechanics■
これまでは、δu がスカラーでした。そして、未知数 u(x,y) もスカラーでしたね。
ポテンシャルや熱問題が、この部類に属します。
ところが、弾性力学になると(流体もそうですが)、未知数もδu ベクトルになってしまいます。
つまり、部分積分法も複雑なってしまうと言うことです。
ですから、頭がくしゃくしゃになりそうな人は、1次元のFEMへ進んでください。
弾性力学になじみのある方は、知っていると思いますが、仮想変位による仕事量は、次の様になっていますよね。
右辺の第1項が領域内部に与えられた外力による仕事量で、第2項が境界にえられた外力による仕事量です。
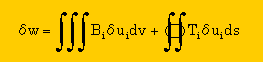 弾性力学では、人の名前の付いた式が沢山出てきます。
下の左は、Cauchy's formula と言って、境界とその直下での出来事を関係付けた重要な式です。
よーく見ると、当たり前な式ですね。
そして、せん断応力は、τij=τji ですから、通常よく見掛ける下の右式が得られます。
ここでも、下の右式をつかいます。
弾性力学では、人の名前の付いた式が沢山出てきます。
下の左は、Cauchy's formula と言って、境界とその直下での出来事を関係付けた重要な式です。
よーく見ると、当たり前な式ですね。
そして、せん断応力は、τij=τji ですから、通常よく見掛ける下の右式が得られます。
ここでも、下の右式をつかいます。
 さて、ここで使う弾性力学でのDivergenceの定理は、Cauchy's formula をベースに、次の様に書くことができますね。
Stressはtensorで、δuiとTiはベクトルですが、下式はエネルギー(仕事)の式ですからスカラーになっていることに注意して下さいね。
だんだん難しくなってきますが、ついてこれる人は、頑張ってついてきて下さい。
"もーいーや"と言う人は、1次元のFEMへ進んでください。
さて、ここで使う弾性力学でのDivergenceの定理は、Cauchy's formula をベースに、次の様に書くことができますね。
Stressはtensorで、δuiとTiはベクトルですが、下式はエネルギー(仕事)の式ですからスカラーになっていることに注意して下さいね。
だんだん難しくなってきますが、ついてこれる人は、頑張ってついてきて下さい。
"もーいーや"と言う人は、1次元のFEMへ進んでください。
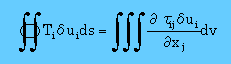 微分ルールを上式の右辺に適用すると、下の様に2つ項に分離できます。今までと同じですね。
微分ルールを上式の右辺に適用すると、下の様に2つ項に分離できます。今までと同じですね。
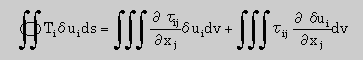
BACK
NEXT
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)