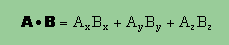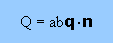Calculus in Finite Element Method
Scalar and Vectors in 2dim and 3dim-2

■Dot Product■
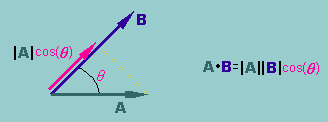
掛け算には、2種類あります。Dot Product と Cross Product です。 Dot Product では、Vector A をもう1つの Vector B に投影したVector をA'とし、|A'||B| を計算します。 計算結果は、スカラーになり、A・Bで表します。 下図に示す様に、|A'|=|A|cos(θ)ですから、A・B=|A||B|cos(θ) と言うことになりますね。

実際に計算するときには、 A=Axi+Ayj+Azk、B=Bxi+Byj+Bzk とすると、下に示す様に、Dot Product は、component毎に掛け算をします。

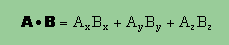Dot Product は、なんかちょっと意味不明の掛け算の様に聞こえますよね。 実は、必要にせまられて、出来た計算なんですよ。では、なぜこの様な掛け算が必要かを考えてみましょう。
例えば、下に示す様に、領域の境界面(a×b)から排出される熱量を計算するときに、Dot Product が使えます。

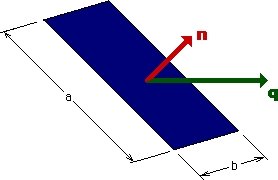Vector n は、面(a×b)に鉛直で長さが 1 になっています。私達は、Unit normal vector と呼んでいます。 Vector q は、面(a×b)から出てくる単位面積当たりの熱流束です。 すると、面(a×b)から排出される単位時間当たりの熱量(Q) は、下の式で計算できることになりますね。

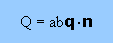ここに、Vector qとn は、下図の様になっています。

もし、qが面abと平行だと、熱は面abから放出されないですよね。つまり、Q=0 ですね。 言い換えれば、qdotn がゼロになっているはずですよね。
BACK NEXT
Menu Fnc Drv Int(1) Dif Crd Chain Lhsptl Vec Green IndxN Int(2)