Gauss-Legendre 積分法による数値積分を紹介する前に、まず、下図を見て下さい。一定要素と違い、Source point は、節点に有ります。図は、Source pointが節点2に有る場合を示しています。一定要素では、要素の中心を節点としましたが、線形要素では、要素の端点を節点としています。そこでは、h_i と q_ni が定義されています。図中の変数については、一定要素のところで説明してありますので、そちらを参考にして下さい。

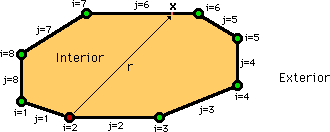
余談ですが、プログラミングでは、節点での境界条件を明白にする必要があります。このことについては、プログラミングの技術で詳しく紹介します。

■G_i1 の計算■
計算を始める前に、既に紹介した Laplace 式の Kernel function と線形要素(Linear element) の形状関数を下に表示します。前回に同じく、r₀=1 そして K=1 とします。

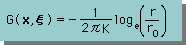
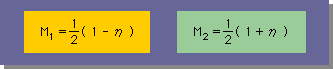
すると、G_i1 は、下式のGauss 積分で計算できます。

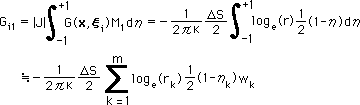ここに、m = Gauss 積分法のサンプリングポイントの数です。r_k は、一定要素で紹介した図に定義してあります。ΔS は、要素の長さです。