参考までに、r logr の不定積分は、0.5r²log_e(r)-0.25r²+cです。すると、G₁₁ と G₁₂ は、次の様に書けます。

Source Point がx₂ の位置ある場合は、どうなるでしょう。答えは、簡単です。上のG₁₁ と G₁₂ が入れ替わるだけです。つまり、結果は、下の様になります。

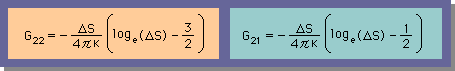
これで要素に関する積分は、全て終了しました。後は、連立方程式を [A]{X}={RHS} の形にまとめるだけです。

■プログラミングの技術■
連立方程式を直接 [A]{X}={RHS} の形にまとめる方法については、既に一定要素のところで説明しました。一定要素の場合は、節点でなく、要素の中央でh(s) とq_n(s) を計算していました。線形要素の場合、要素上のh(s) とq_n(s) を線形で近似します。したがって、離散化のために、h₁とq_n1、それにh₂とq_n2 の2点が要素上に必要になります。それらのベストチョイスが、節点です。

節点は、要素と要素の節目の点です。ということは、節点において、2つの要素の境界条件が融合することになります。この境界条件を正確に把握させるプログラムを書かないと、とんでもない計算結果を出力することになります。例えば、要素1がDirichlet型で要素2がNeumann型の境界条件の場合、二つの要素がリンクされる節点の境界条件は何かです。次のページに、実際プログラムで使っている要素の境界条件と節点の境界条件を示します。