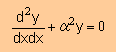
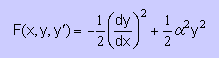
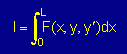
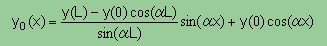
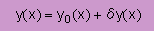 ここにδy(x)=δy1φ1(x)
ここにδy(x)=δy1φ1(x)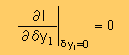
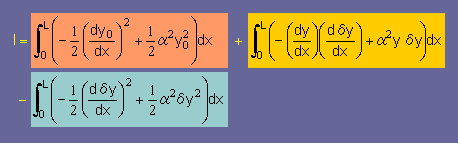
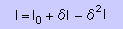
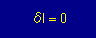 だね
だね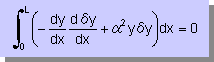 である
である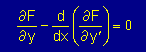
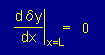
■Calculus of Variations のまとめ■
有限要素法の勉強の中で特に注意してもらいたい項目が幾つかあります。
それらは変分法、Divergenceの定理、座標変換が有ります。
中でも変分法は しっかりと勉強して下さいね。
重み付け残差法とかGalerkin法とかEnergy法とか色々な方法が有りますが それらはぜんーぶ変分法から導き出されているのです。
| Helmholtz Equation と その状態関数 | 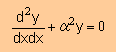 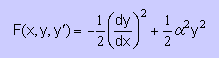 |
| 変数y(x)のpathを変えながら右の積分を計算します。 積分値が最大か最小(つまり極値)になるときがHelmholtz Equationの厳密解になる。 | 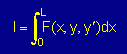 |
| 両端がDirichlet型境界条件のとき、厳密解はy0(x) になる。 このとき積分は I0になる。 | 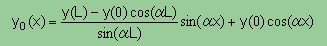 |
| 変数y(x)のpathを変えるために むりやり近似式(近似解)を作る | 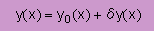 ここにδy(x)=δy1φ1(x) ここにδy(x)=δy1φ1(x) |
| 極値はIをδy1で微分してゼロになる点になる。 この場合δy1もゼロなる。 | 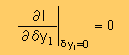 |
| ここでは近似式を状態関数に代入してIがI0になる条件を探す。 | 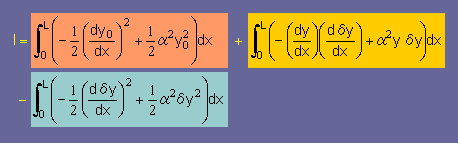 |
| ショートハンドで上の式を書く。そして IがI0になる条件を探す | 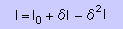 |
| IがI0になる条件は | 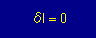 だね だね |
| つまりδI=0 とは | 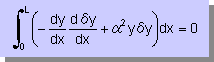 である である |
| 上の式は、重み付け残差法で導いた式と同じですね。 近似式と重み関数の定義する、 積分式を定義しゼロと置く、積分式の2階微分項に部分積分法を施す と言う操作をやったのと同じ結果が得られたことになる | |
| 近似式を構成しているδy(x)が重み関数になっている。 これは近似式に一部を重み関数とするというGalerkin法と同じ結果になっていますね | |
| Euler-Lagrange Equation は状態関数と微分方程式との架け橋である | 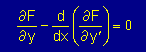 |
| 重み関数の微分はNeumann型境界でゼロになる | 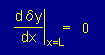 |