One Dimensional Finite Element Method
Parabolic Element
■1次元2次要素■
1次元有限要素法のしめっくくりとして2次要素を紹介します。
ここで私が紹介している事柄をマスターしますと貴方自身の力で、3次、4次、5次要素で Helmholtz Equation の解析が出来るようになります。
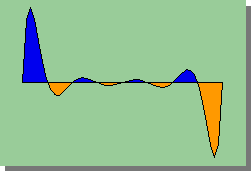
高次要素の欠点は要素端点での近似解の乱れです。
次数が高くなると どうしても要素の両端点付近の近似解が大きな値を示すようになります。
下の図に示すグラフがそうです。
弾性解析に高次要素を使うと このような問題に遭遇し 要素端点での応力の計算に大きな誤差を招く要因になっています。
応力は、変位の微分ですから ますます大きな値になってしまします。
私は個人的に静解析は2次要素まで そして時間依存は1次要素までとしています。
そして解析精度を向上させるには要素分割数を多くしています。
それでは早速 2次要素を勉強してみましょう。
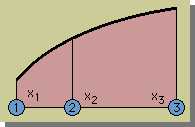
下図が2次要素です。
円の中の数字が節点番号です。
 まず1次要素と同様に近似式と形状関数の作成から始めます。
下は 2次要素の近似式になります。
まず1次要素と同様に近似式と形状関数の作成から始めます。
下は 2次要素の近似式になります。
|
u(x) = N1(x) u1 + N2(x) u2 + N3(x) u3
|
上のN1(x)、 N2(x)、 N3(x)は2次要素の形状関数です。
1次要素と同様に形状関数は
守らなくてはならない条件が有ります。
下がそうです。
| N1(x)= | 1 | at x = x1 |
| 0 | at x = x2 |
| 0 | at x = x3 |
|
|
| N2(x)= | 0 | at x = x1 |
| 1 | at x = x2 |
| 0 | at x = x3 |
|
|
| N3(x)= | 0 | at x = x1 |
| 0 | at x = x2 |
| 1 | at x = x3 |
|
上の条件を1筆で書くとNi(xj) = δij となります。
δij は i=j のときだけ1で その他は全てゼロになります。
BACK to Variational Calculus
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method


