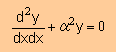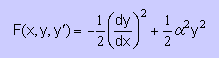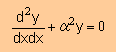
■変分法(Calculus of Variations)■
なんとなく雰囲気はつかめてもイマイチ理解出来ないのが変分法です。
ここでは一番簡単な例を取り上げて変分法を説明しています。
このセックションを読み終わるころには貴方も変分法の概要が理解出来る様になっていると思いますよ。
変分法では時間、長さ、面積、エネルギー等のスカラー量を表す状態関数と言う関数が必要になってきます。 変分法の結果からは単なるスカラー量でなく物の形状を表す関数(y(x))が得られます。 その y(x) で表された形状を変えながら 状態関数 を領域積分し積分値が極値(最大または最小)になる様に解(y(x))を導く方法のことを変分法と言います。 ちょっとピンと来ない人のために代表的な問題例を下の表にまとめて有りますので参考にして下さい。
| 問 題 | 目 的 | 答 え |
|---|---|---|
| BRACHISTOCHRONE | 球が位置Aから位置Bまで転がり落ちるのに必要な時間が最小になる曲線を見つけ出したい | サイクロイド曲線 |
| GEODESIC | 3次元空間の2点間の距離が最小になる曲線を求めたい | 直線 |
| ISOPERIMETRIC | 限られた長さの糸で輪を作りそれを平面上に置き糸の輪の内側に出来る面積を最大にする輪の形を求めたい | 円 |
| ELASTOSTAIC | 静荷重が負荷されている構造物の変位を知りたい | 歪エネルギーが最小な状態 |
| RESIDUAL | 微分方程式の解を知りたい | 残差が最小 |
上の表をよーく見ると答えが単なる値ではありませんね。 どちらかと言うと水平思考的な考え方の問題になっていますね。 上表の最後の問題は目的と答えが逆になっていますね。 変分法が発達してくると”何を最小にすると目的のものが得られるか”と言う風に考え方が変わってきています。
ここで紹介している学問のことをCalculus of Variations (1697年から)と言いJean Bernoulli (1667-1748) が先駆者と言われています。
(Bernoulliと言う名前はよく耳にしますが一人ではありません。)
これに対して Isaac Newton (1642-1727) が造った学問を Calculus (1665年から) と言います。
Calculusでは力のバランスから微分方程式を導きその微分方程式を直接解く方法を学びます。
変分法では与えられた問題の中に最大か最小にできる変数を探します。
技術分野ではエネルギーがその代表例です。
その変数を 状態関数 と言う関数で表します。
その関数を領域積分し積分結果が極値(最大または最小)になる解(形状)を導きます。
■Helmholtz equation の 状態関数■
これまではHelmholtz equation を解いてきましたね。
ここでも両端をDirichlet 境界として下式の Helmholtz equation を解くことにします。