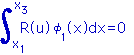 |
で連立方程式の第1行(Row)が出来上がる。 |
 |
で連立方程式の第2行(Row)が出来上がる。 |
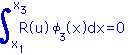 |
で連立方程式の第3行(Row)が出来上がる。 |
■要素ごとの積分■
これまでに紹介してきた積分式の計算方法では積分範囲が常に全領域でした。
そのために近似式と重み関数は全領域をカバーしている必要がありました。
また下の積分式を用いて連立方程式を行単位で作成していました。
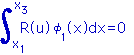 |
で連立方程式の第1行(Row)が出来上がる。 |
 |
で連立方程式の第2行(Row)が出来上がる。 |
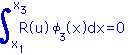 |
で連立方程式の第3行(Row)が出来上がる。 |
さて、どうすれば機械的に積分式が計算出来るのでしょうか。 貴方がプログラムを書くとすれば、どのように書くか考えてみて下さい。 答えは簡単です。 要素毎に積分式を計算すれば良いのです。 考え易くするために上の積分式をもう少し詳しく下図に書き直してみました。
