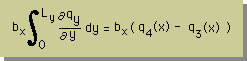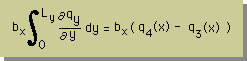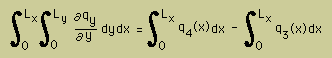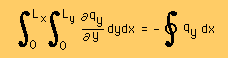Calculus in Finite Element Method
Green's Theorem-3
y方向の熱流束(qy)もx方向と同様に、まず、幅bxの部分の積分から始めます。
下に、式を示します。
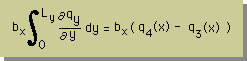 幅bxは、とても狭いものと仮定してあります。
幅bxは、とても狭いものと仮定してあります。
次に幅bxをLxを広げるために、上の式の両辺を、0からLxまで、x方向に沿って積分します。
左辺は、面積(領域)積分になり、右辺は線積分になります。
下に積分結果と、線積分を行う部分と方向を示します。
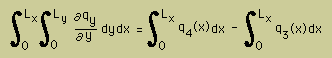
 次に、上式の右辺の第2項の積分方向を逆にします。すると、線積分方向が時計回転になります。
下がその積分の式と線積分の方向です。
次に、上式の右辺の第2項の積分方向を逆にします。すると、線積分方向が時計回転になります。
下がその積分の式と線積分の方向です。

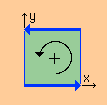
 線積分は反時計方法がプラスですから、上の線積分を閉じた線積分の記号で表わすには、下の左図に示すように、
線積分の記号の前にマイナスが必要になります。
つまり、マイナスと線積分の記号で、下の右図に示すの線積分方向になります。
線積分は反時計方法がプラスですから、上の線積分を閉じた線積分の記号で表わすには、下の左図に示すように、
線積分の記号の前にマイナスが必要になります。
つまり、マイナスと線積分の記号で、下の右図に示すの線積分方向になります。
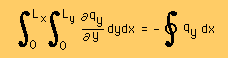
BACK
NEXT
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)