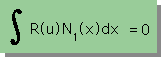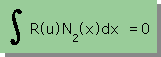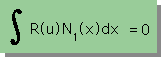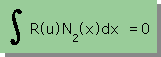One Dimensional Finite Element Method
Integral By Element-2
前ページの図を観察すると要素毎に次の様な計算を行っています。
要素ごとの計算の手続きは、まったく同じで違うのは変数α2と要素の長さのみになります。
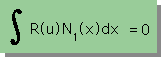 |
と |
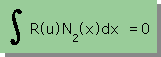 |
上の積分式は、=0 となっていますが
前ページの2番目の積分式の各々の項は、=0 とはなっていないことに注意して下さい。
この違いは後で説明する
Inter-Element Continuityと呼ばれている要素間の条件と深い関係があり、この条件が満たされた時に
前ページの2番目の積分式と上の積分式は同じになります。
ここではとりあえず要素ごとに上の積分式を計算してみて下さい。
計算結果を連立方程式の適切な場所に足し込めば行単位で作成した式と同じ連立方程式が出来がります。
この足し込みの操作のことをAssemblyといいます。
まだちょっと理解が出来ていない貴方のために3つの重み関数
φ1,
φ2,
φ3
を1つのグラフに重ねて書いてみて下さい。
下図の様になるはずです。
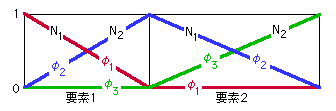
上図に示す様に各々の要素に形状関数 N1(x) と N2(x) が現われているのに気付くと思います。
■要素1での積分■
それでは早速、要素ごとの積分を実施してみましょう。
まず計算を進める前に要素1に関係する変数を書き出してみましょう。
下図にそれらを示します。
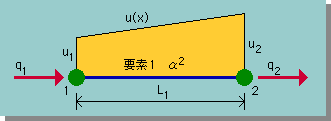
節点1に未知数u1とNeumann境界条件の境界値である q1 が割り当てられています。
同様に、節点2にもu2とq2 が存在しています。
そして要素を特徴付ける要素長さ
L1と
α2も有ります。
さて、これらを使って要素1に関係する積分式を計算してみましょう。
次の様になります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method