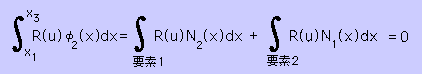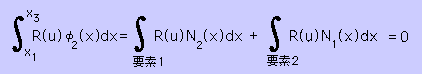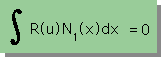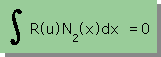One Dimensional Finite Element Method
Integral By Element-9
■Inter-Element Continuity■
要素毎の積分のセックションを離れる前に∫R(u)φ2(x)=0 の積分式について、もうちょっと、伝えておきたいことがあります。
まず下の式を御覧下さい。
 |
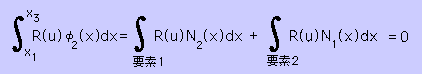| 第1の方法と呼ぼう |
この積分式は、本セックションの最初のページ(2番目の式)に出てきましたね。
上の式ではφ2(x)を1つの領域全体をカバーする関数として積分しています。
話を進め易くするために、ここでは上の式を第1の方法と呼ぶことにします。
しかしいままでの説明では下の2つの積分式を別々に計算し連立方程式へ足し込め(Assembly作業)ばいいと書いてありましたね。
これを第2の方法と呼ぶことにします。
すると、ここで説明している2つの計算方法は矛盾していることになりますね。
 |
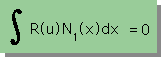と |
 |
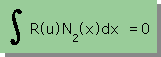| 第2の方法と呼ぼう |
第2の方法ですが上の2つの積分式を計算し連立方程式へ足し込むという操作(Assembly作業)は次の様に書き表すことができます。
なんとなく無理な表現ですが勘弁して下さい。
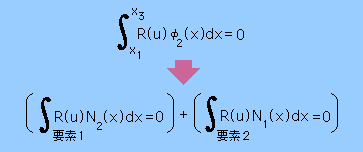Assembly作業を行うと言うことは未知数 u1, u2, u3 で積分結果をくくることになりますね。
理屈上、第2の方法と第1の方法からは同じ結果が得られなければならないはずですよね。
しかし計算を進めると右辺に違いが残ります(詳細は次のページに)。
では2つの計算方法(第1と第2の方法)はどの様な条件であれば同じになるんでしょうか。ちょっと考えてみましょう。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method