■有限要素法のターミノロジー■
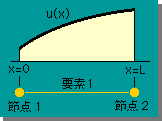
先へ進む前に有限要素法のターミノロジーを少々紹介しておきます。下図を見て下さい。

1つの要素(Element)が描かれています。未知数(u(0) または u(L))が与えられている点を節点(Nodal point)と言います。つまり、解析を行うと、節点での未知数の値が計算されます。節点間の未知数(u(x))は、これまでに紹介してきた近似式で表します。そして、その近似式は、形状関数(Shape Function)で構成されています。

■2つの1次要素■
1つの要素を用いてHelmholtz Equation を解くためには、これまでに説明してきた様に、近似式の関数は、Helmholtz Equation のα²をは反映させるため、2次曲線でなくてはなりません。言い替えると、1次要素を1つ使って未知数を表すと、α²の入り込む余地は、ないということになります。 すると、1次要素を使った場合、α²を反映させるために、最低、領域をどの様に表わ せば良いか考えてみましょう。答えは、下図に示す通りである。

領域を2つの1次要素で分割すると、領域の中央付近でα²が反映される u₂が計算されるようになります。

この場合、近似式は連続であるが、近似式の微分はx₂の点で、不連続になります。一般に市販されている応力解析ソフトから出力される応力が不連続になっているのは、この近似式が起因しているためです。つまり、この不連続が誤差の原因の1つといえます。また、この不連続を、出来るだけ小さくすることが、精度向上につながるのです。

応力を連続にする方法もあります。それは、Hermite Interporation と呼ばれる形状関数で構成されている有限要素法です。未知数として、u(x)以外に du(x)/dx があります。一時期、沢山の文献が出ましたが、現在では未知数が2倍になるということと、プログラムが複雑になるという理由から、市販ソフトでは殆ど使われていません。時間があれば、Hermite Interporation を紹介したいと思います。