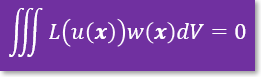
■Boundary Element Method■
有限要素法と、ほぼ同時期に開発が進められた方法があります。現在では、境界要素法(Boundary Element Method(BEM))として知られています。有限要素法の領域型に対し、境界要素法は境界型です。つまり、境界を要素分割することで、解析が可能になるため、Input Dataを大幅に削減出来るというメリットがあります。
その他、有限要素法にない特徴として、無限領域があります。波や振動等の減衰を取り扱う場合、有限領域だと境界からの反射波が解析値の誤差を大きくすることもあります。

境界要素法は、画像処理技術でよく用いられる Green's FunctionとGreen's Identityを含むGreenの定理が基礎になっています。Divergence Theoremは、最もよく知られたGreenの定理です。

Greenの定理を完成させたGeorge Green(1793-1841)は、40歳でCambridge大学へ入学し、48歳でこの世を去っています。大学に4年在籍したとして、彼は残り4年間でこのGreenの定理を完成させている計算になります。実際には、大学への入学前にGreenの定理に関する論文を出している。Green自身は、境界要素法は作り出しているわけではありませんが、Greenの定理を完成させるまでに様々なトライをしたことは間違いないでしょう。Greenのトライは、次の積分式と下表の関数w(x)を考慮したと考えられます。

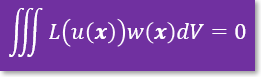
関数　w(x)	積分式の意味
w(x)=0	Trivial Solution
w(x)=Constant	差分法(正確には積分型差分法)
w(x)=Linear or Higher	有限要素法
w(x)=Green's Function	境界要素法

Green's Functionを上の積分式に代入し、部分積分を2回行うと上の積分式は、境界積分に変換されます。参考までに、L(u(x))が2次元Laplace eq. の場合、w(x) = log_e(1/r) になります。

境界要素法は、境界積分を数値的に計算し、近似解を得ています。このとき、境界は要素に分割されていなくてはなりません。有限要素法に比べ、決定的な違いは、積分の次元が1つ少ないことです。既に、現在では、この特徴を生かし技術解析の道具として使われ始めています。

境界要素法の弱点としては、支配方程式を満たすFndamental Solution が必要なため、解析に限界があることです。特に、支配方程式が非線形の場合は、解析が不可能になることがあります。また、時間依存の場合も、解析手順が複雑になります。逆に長所としては、解析精度がきわめて高いことです。

以上、有限要素法やその周辺技術の発展の歴史について述べてきました。まだまだ、書き足らない部分はありますが、これ以上内容を深めても泥沼状態になるだけで、FEMの理解には何のプラスにもなりませんので、ここらへんで止めます。もっと歴史について知りたい方は、下の文献を参考にしてください。
Huebner, Segerlind, Gallagher, Beckmann, Martin and Carey, Dym and Shames Banerjee and Butterfield

最後に、力学と数学の歴史を簡単に1つの絵にまとめてみました。 ここをクリックしてみて下さい。