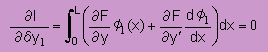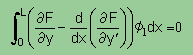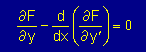そして、y(x) と　y'(x) を　δy₁ で微分すると、下の様になります。

結果的に、I　をδy₁ で微分した積分式は、次の様に書けます。

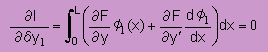上式の第1項には、φ₁　がかけられていますが、第2項には、φ₁の微分が掛け算されています。微分の階数を揃えるために、第2項に、部分積分を施します。すると、次の様になります。

結果的に、積分式は、次の様になります。

領域の両端の境界条件は、Dirichlet でしたから、φ₁(0)=φ₁(L)=0 になります。したがって、上の積分式は、下の様な、WRM の基本式と同じ形になります。

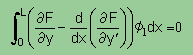領域の長さは、任意ですから、次のことも言えます。

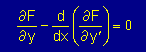
上の式のことを、Euler-Lagrange Equation と言い、 y(x)が極値になる為の必要条件(∂I/∂δy₁=0 またはδI=0)を満たしていることになりますよね。

この式については、まだ先がありますが、WRMの理屈を知る上では、ここらへんで止めておきましょう。”私は勉強してみたいなー”と思っている貴方は、大学等の図書館や書店で変分法についての本を読んでみて下さい。

ここでは変分法の理屈よりも、ここで導いたEuler-Lagrange Equation が正しいかどうかをチェックしてみましょう。