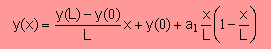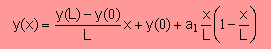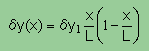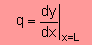One Dimensional Finite Element Method
Calculus of Variations-10
例としてDirichlet 境界条件のHelmholtz equation の近似解は次の様な式で表していましたよね。
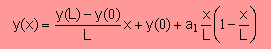 ここに a1 は有限要素法の解析で求まる定数でしたね。
ここに a1 は有限要素法の解析で求まる定数でしたね。
これまでの議論ですと上の近似解は、厳密解+重み関数(y0(x)+δy(x)) ですから δy(x)が含まれていることになりますよね。
ですから上の式からδy(x)の条件(Dirichletだからδy(0)=δy(L)=0) に合う関数をpick up することにより重み関数を作れますね。
つまり下式です。
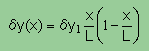 この様に近似解の一部を重み関数として流用する方法を Galerkin method と呼びます。
都合の良いことに近似解の式を構成している形状関数と重み関数を作り上げている形状関数の条件が同じだからです。
まー重み関数を作る手間が省けると言うことですね。
この様に近似解の一部を重み関数として流用する方法を Galerkin method と呼びます。
都合の良いことに近似解の式を構成している形状関数と重み関数を作り上げている形状関数の条件が同じだからです。
まー重み関数を作る手間が省けると言うことですね。
■Neumann Type B.C.■
これまではDirichlet 境界条件のみを扱ってきました。
ここではNeumann Type の境界条件について簡単にふれておきます。
Neumann Type の境界においては dy/dx が境界値として与えられることになります。
Helmholtz equation では左右対称の条件がそうでしたね。
一般的に下式で Neumann Type の境界条件は与えます。
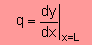 上の式の場合は x=L の境界がNeumann Type の境界になっています。
ということは y(L)は、q の値によって変動することになりますね。
また q が一定でも近似解(y(x)=y0(x)+δy(x))の精度によっても y(L) は変化します。
ですから δy(L)は下図(次のページ)に示す様に Neumann Type の境界において ゼロにならないことになります。
上の式の場合は x=L の境界がNeumann Type の境界になっています。
ということは y(L)は、q の値によって変動することになりますね。
また q が一定でも近似解(y(x)=y0(x)+δy(x))の精度によっても y(L) は変化します。
ですから δy(L)は下図(次のページ)に示す様に Neumann Type の境界において ゼロにならないことになります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method