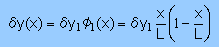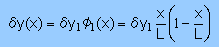例題を作るにあたって問題になるのが、上式のδy(x) または φ₁(x) の決めかたです。ところが、先程も言った通り、変分法では、δy(x) について、何の記述もありませんでしたね。と言うことは、勝手に決めて良いということになります。ただ、両境界条件が、Dirichilet型ですから、δy(0)=δy(L)=0 になります。これは、境界条件からくる規制ですから、δy(x) そのものの条件ではありません。

と言うことで、δy(x)は、勝手に決めて良いことになります。そこで、ここでは、前に使ったことのある下式を使ってみます。

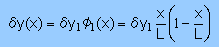いかげんだなー、とお思いでしょうが、これが変分法です。逆に、δy(x)に規制がないと言うことは、それだけ自由度が有ると言うことです。数値解析を行う上では、有利なことですよ。 では、早速、計算してみましょう。下の左の図を見て下さい。δy₁ (図の横軸)をゼロから1.3まで変化させて、状態関数 を積分(図の縦軸)してみました。もちろん、積分区間は、x=0からx=Lです。計算には、Program 状態関数.for を使いました。

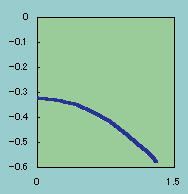
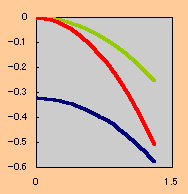確かに、δy₁=0 で、積分式の値(I)は、最大になっていますね。ついでに、δIとδ²I も計算してみました。上の右の図がそうです。δy₁=0 で、δI=0 になっていますね。δIとδ²Iの計算には、それぞれ、Program deltai.for と Program deltasqi.for を使いました。貴方も計算してみて下さいね。

■Galerkin Method と 重み関数(δy(x))■
これまでは、厳密解(y₀(x)) が有るものとして、話を進めてきました。が、実際の有限要素法の解析において、厳密解は、存在しません。したがって、近似解(y(x)) の式は、作れるけれども、重み関数(δy(x))は、そー簡単には作れません。