Theory-Torsion

Torsion
Governing Equations By Kinematics

■2次元Torsionの概念■
断面が任意の均一柱形シャフトのTorsionはシャフトの一端を固定し他端にモーメントを与えれば 3次元弾性解析でねじれ角(Angle of TwistまたはTwist)とねじれ率θ(Rate of Twist)を得る頃が出来ます。しかし、ねじれはせん断応力のみがシャフトに発生しているため、ひずみ(Strains)や応力を式で表すことが出来ます。この考えから3次元シャフトの任意断面の2次元解析が可能になっています。

そこでTorsionについて過去の文献(本)を調べてみました。参考にしたのが本が以下の4つです。

Torsionの解析の話は円柱から始まります。Twist(ねじり)された円柱の断面は力を掛ける前と同じという条件を付ければExact解が得られています。Twist時、円柱に変形が無いという条件も追加されています。 SegerlindはTorsionについての式の展開は無いが、以下のTorsionの支配方程式と境界条件をベースに変位法の有限要素法で解く手順を紹介しています。

\begin{eqnarray} \ Governing \ Equation \ : \frac{\partial^2\phi}{\partial x\partial x}+\frac{\partial^2\phi}{\partial y\partial y}=-2G\theta \end{eqnarray}

\begin{eqnarray} \ Boundary\ Condition\ : \phi=0\ along\ the\ boundary\ of\ the\ shaft \ cross \ section \end{eqnarray}

\begin{eqnarray} \ Applied \ Moment \ : M=2\iint\phi dA \end{eqnarray}

Torsionの解析で出てくる定数および未知数を以下にまとめておきました。使っているシンボルは文献により異なります。

G=Shear Modulus
β=ねじれ角=シャフトの回転角(Angle of Twist or Twist)
θ=単位長さ当たりのシャフトの回転角(Rate of Twist)
φ=Stress function
M_z=シャフト端部z軸周りでのモーメント

上で示しているθはシャフトの長手方向の座標がzだと、β=θzですからθは以下の様に定義出来ます。 \begin{eqnarray} \theta=\frac{\partial \beta}{\partial z} \end{eqnarray}

■Saint Venant theory■
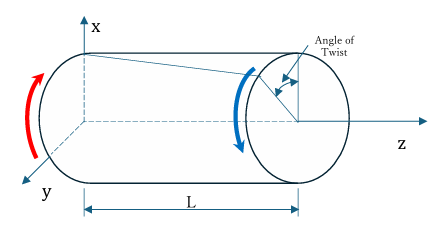
Dym and Shamesは Saint Venant theory の仮定を用いTotal Potential EnergyとTotal Complementary EnergyからVariational process に落とし込み、上の微分方程式と境界条件を導いています。 TimoshenkoもSaint Venant theoryの仮定をベースに上の微分方程式と境界条件を導いています。ただし上の微分方程式の導出についてVariational等は使っていません。ただ、上の微分方程式と境界条件に至るまでの歴史上の展開が詳しく記載されています。ここではTimoshenkoをベースにTorsionの微分方程式の導出を試みてみます。下図は円筒ですが断面が任意の均一柱形シャフトだと思って下さい。シャフトの長さはLとします。両端の図に示す様なモーメントが作用しています。座標の原点は左端にあります。

両端の上図の様にペアーモーメントがシャフトに有る場合のTorsion問題はSaint-Venantによって正解が導かれています。

Saint-Venantの仮定は次の2つから成り立っています：

回転を与えられたシャフトの断面の変形は円筒シャフトの断面と同じ
断面の反り(warping)は全ての断面で同じ

上図のように座標の原点を左端とすると、回転断面での変位は次の様になります。 \begin{eqnarray} u=-\theta zy \end{eqnarray} \begin{eqnarray} v=\theta zx \end{eqnarray} ここにβ=θzは座標値z面での断面のねじれ角(Angle of Twist)になります。断面での反り(warping)は関数ψを導入すると次の様に定義できる。 \begin{eqnarray} w=\theta\psi\left(x,y\right) \end{eqnarray}

Saint-Venantは問題の解決にSemi inverse methodを使っていています。 Semi inverse methodとは、上の仮定を用い下の平衡式(B_i=0の場合)(Navier' Equations)とその境界条件(Cauchy's formula)を満足させ微分方程式を構築するために使用されます。

\begin{eqnarray} \frac{\partial\tau_{ij}}{\partial x_j}+B_i=0 \end{eqnarray}

\begin{eqnarray} T_i=\tau_{ij}n_j \end{eqnarray}

このTorsion問題に関しては、以下の仮定が事前に与えられています。Torsionはせん断応力のみが発生するので、以下は正しいと言えます。また後で紹介する３次元弾性解析でも確かに以下は成立します。

\begin{eqnarray} \varepsilon_{xx}=0 \end{eqnarray}

\begin{eqnarray} \varepsilon_{yy}=0 \end{eqnarray}

\begin{eqnarray} \varepsilon_{zz}=0 \end{eqnarray}

\begin{eqnarray} \gamma_{xy}=0 \end{eqnarray}

すると、γ_xzとγ_yzがnon-ZEROとして残ることになります。結果的に平衡式は下のようになります。

\begin{eqnarray} \frac{\partial\tau_{xz}}{\partial z}=0 \end{eqnarray}

\begin{eqnarray} \frac{\partial\tau_{yz}}{\partial z}=0 \end{eqnarray}

\begin{eqnarray} \frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}=0 \end{eqnarray}

上の１と２番目は、仮定より剪断力はzの関数でないので満足しています。3番目は後ほど触れます。

上で示した仮定からγ_xzとγ_yzは次の様になります。

\begin{eqnarray} \gamma_{xz}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}=\theta\left(\frac{\partial\psi}{\partial x}-y\right) \end{eqnarray}

\begin{eqnarray} \gamma_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}=\theta\left(\frac{\partial\psi}{\partial y}+x\right) \end{eqnarray}

よって応力はGγより次の様になる。

\begin{eqnarray} \tau_{xz}=G\theta\left(\frac{\partial\psi}{\partial x}-y\right) \end{eqnarray}

\begin{eqnarray} \tau_{yz}=G\theta\left(\frac{\partial\psi}{\partial y}+x\right) \end{eqnarray}

これらをBody forceの無い平衡式∂τ_xz/∂x+∂τ_yz/∂y=0に代入すると以下のLaplace微分方程式になる。

\begin{eqnarray} \frac{\partial^2\psi}{\partial x\partial x}+\frac{\partial^2\psi}{\partial y\partial y}=0 \end{eqnarray} この式の境界条件としてはシャフトの表面には外力が存在していないという事実からτ_nn=0になっていなければなりません。つまり下式になります。Normal vector n_jについては、 Calculusを参考にして下さい。 \begin{eqnarray} {\tau_{jz}n_j=\tau}_{xz}n_x+\tau_{yz}n_y=\left(\frac{\partial\psi}{\partial x}-y\right)\left(\frac{dy}{ds}\right)+\left(\frac{\partial\psi}{\partial y}+x\right)\left(-\frac{dx}{ds}\right)=0 \end{eqnarray} 式中のθは右辺が=0ですのでドロップしてあります。これはNeumann型の自然境界条件ですので、上のLaplace微分方程式を解くには少なくともDirichlet境界条件が必要になります。Dirichlet境界条件について明確な式が示されていないので上のLaplace微分方程式を解くことができません。Total Potential Energy Methodでも同様な結果になっています。
しかしDirichlet境界条件が見つかれば反りの変位量は、定義から以下の式で計算出来ます。今後 3次元弾性解析-Torsion のところでシャフトの長手方向の変位を調査し、確かなDirichlet境界条件が見つかれば境界要素法-Torsionで反りの変位量の計算を試みます。

\begin{eqnarray} w=\theta\psi\left(x,y\right) \end{eqnarray}

■Stress functionφ(x,y)をベースにしたTorsionの式の導出■
ということでTorsion問題の解析には上のシャフト断面のWarpingを取り入れた方法でなく、上で紹介した2つの剪断力をStress functionφ(x,y)で表した方法が紹介され、これが最も有限要素法向きに解析手順になっています。この方法はまずBody forceの無い平衡式\begin{eqnarray}\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}=0\end{eqnarray}を満足する下のStress functionnφ(x,y)を作るところから開始している。

\begin{eqnarray} \tau_{xz}=\frac{\partial\phi}{\partial y}=G\theta\left(\frac{\partial\psi}{\partial x}-y\right) \end{eqnarray}

\begin{eqnarray} \tau_{yz}=-\frac{\partial\phi}{\partial x}=G\theta\left(\frac{\partial\psi}{\partial y}+x\right) \end{eqnarray}

確かに上の２式を\begin{eqnarray}\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}=0\end{eqnarray}へ代入すると結果ゼロになります。次にやることは”Warping function”を上の2つの剪断力の式から取り除くことです。 Timoshenkoによると割と荒っぽい方法を使っています。まず、τ_xzをyで微分します。次にτ_yzをxで微分し最初の微分から差し引きます。結果を少しアレンジすると以下の Poisson's Equation が得られます。

\begin{eqnarray} \frac{\partial^2\phi}{\partial x\partial x}+\frac{\partial^2\phi}{\partial y\partial y}=-2G\theta \end{eqnarray}

そして境界条件はシャフトの側面に外力が働いていないということから T_in_i=0 を満足していなければならない。つまりdφ/ds=0となる。

\begin{eqnarray} \tau_{jz}n_j=0 \end{eqnarray}

τ_jzn_j を展開すると以下になります。 \begin{eqnarray} {\tau_{jz}n_j=\tau}_{xz}n_x+\tau_{yz}n_y=\frac{\partial\phi}{\partial y}\left(\frac{dy}{ds}\right)-\frac{\partial\phi}{\partial x}\left(-\frac{dx}{ds}\right)=\frac{\partial \phi}{\partial s}=0 \end{eqnarray} 結果的に \begin{eqnarray} \frac{\partial \phi}{\partial s}=0 \end{eqnarray}

結果の∂φ/∂s=0は言い換えると境界でφ=一定ということになる。したがってφ=0としても問題なさそうです。したがって上のPoisson's Equationを境界条件

\begin{eqnarray} \phi=0 \end{eqnarray}

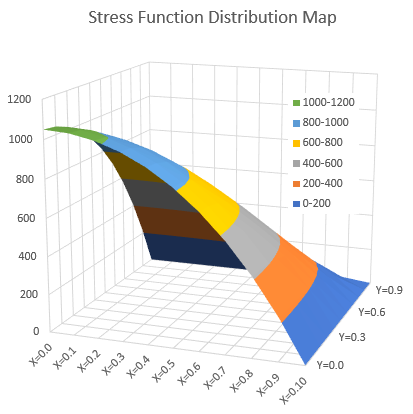
で解けばシャフトの剪断力を得ることができます。下は矩形断面の1/4を有限要素法で解いたφです。 G=26538461.5384615[Pa], θ=0.0000670055862315403で計算した結果です。詳細は後ほど紹介します。

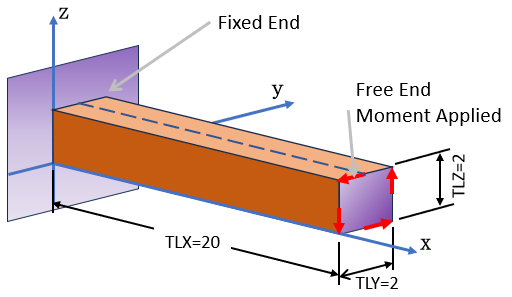
このTorsion問題ですが、シャフトの単位長さ当たりのねじれ角を与えたときに変位と応力が計算できる方法を提案しています。弾性力学の場合は下図に示す様に、シャフトの左端を完全拘束し、右端にねじれを発生させるモーメントM=4000[Nm]を与えます。そしてシャフト内の長手方向に対し直角の変位(w(x,0,1)=図の破線の位置の変位)からねじり角を計算します。

このTorsion問題の場合、Stress functionφ(x,y)の定義からせん断応力は計算できますが、ねじりを発生させるモーメントMはどのようにすれば得られるのでしょうか。シャフトに蓄えられているエネルギーを計算すると簡単に計算出来そうです。まずシャフトにねじれを与えている端部のモーメントをエネルギーで表すと以下になります。 \begin{eqnarray} \pi_M=ML\theta \end{eqnarray} L=シャフトの長さです。シャフトの端部の面にのせん断応力(τzx, τzy)によるエネルギーは次の様になります。 \begin{eqnarray} \pi_\tau=\iint{u_iT_idA}=L\theta\iint\left(-y\tau_{zx}+x\tau_{zy}\right)dA \end{eqnarray} \begin{eqnarray} \pi_M=\pi_\tau \end{eqnarray} より \begin{eqnarray} M=\iint\left(-y\tau_{zx}+x\tau_{zy}\right)dA \end{eqnarray} 上式のせん断応力の代わりにStress functionを代入すると以下になります。応力のτzx=τxz , τzy=τyzに注意。

\begin{eqnarray} M=\iint\left(-y\frac{\partial\phi}{\partial y}-x\frac{\partial\phi}{\partial x}\right)dA=-\iint{x_i\frac{\partial\phi}{\partial x_i}dA} \end{eqnarray}

部分積分法を適用すると

\begin{eqnarray} M=-\iint{x_i\frac{\partial\phi}{\partial x_i}dA=-\left(\oint{x_i\phi ds}-\iint{\phi\frac{\partial x_i}{\partial x_i}dA}\right)} \end{eqnarray}

境界でφ=0です。そして∂x_i/∂x_iは2次元で2ですから、最終的にMとして以下が得られる。

\begin{eqnarray} M=2\iint\phi dA \end{eqnarray}

上で導かれたTimoshenko によるPoisson's Equationですが、Total Complementary Energyを使った式の展開でも同じPoisson's Equationが得られています。これまでにTorsionの微分方程式(Poisson's Equation)を導いてきましたが、なんとなくすっきりしないのが現実です。出来ればAnalyticallyに且つstraightforwardにTorsionの支配方程式を導きたいものですね。

この問題ではTotal Potential Energy Methodを使うと最終的に断面での反り(warping)関数ψのLaplace Equationが導き出され、Total Complementary Energyを使うとStress FunctionのPoisson's Equationが得られました。これは問題をEnergy 等を使ってKinematics的に導いているからです。何が問題だったかと言うと、円柱の場合は反り(warping)が発生しないが、任意断面になるとwarpingが発生し問題を複雑にしています。

議論はこれまでとして、とにかくPoisson's Equationを2次元有限要素法で解いてみましょう。そして3次元弾性力解析で同じ問題を解いてみます。3次元弾性力解析ではShear Modulusとモーメントを与えRate of Twistのθを算出します。 Poisson's Equationを2次元有限要素法では、Shear ModulusとRate of Twistのθを与えるとモーメントが算出されます。このモーメントが3次元弾性力解析で与えたモーメントと同じならTorsion理論は成立していることになります。

また、当たり前ですが3次元弾性力解析の結果からはWarping(シャフト長手方向の変位)も得られます。そして反り(warping)関数ψのLaplace Equationを解くとθψから反り量が得られます。これら2つを比較することにより理論の整合性が判明します。

以上の様に、ここでは有限要素法と境界要素法で解いてSaint Venant theoryを確かめてみます。計算結果のチェックには、Saint Venant theoryのベースになっている3次元弾性解析を使います。

Menu Theory-Torsion FEM-Torsion BEM-Torsion 3DIM-Torsion

Internet College of Finite Element Method