■境界要素法でTorsionのPoisson’s equationを解く■
境界要素法で今回の問題を解いてみました。
と言いてもPoisson’s equationのGreen関数は無いのでLaplace EquationのGreen関数を使い、2Gθは領域積分します。
通常、境界要素法では境界のみを要素分割しますが、今回は領域も要素分割する必要があります。
境界要素法は有限要素法の重み付け残差法と同様に、下式に示す様に残差×重み関数の領域積分からスタートします。
| \begin{eqnarray} \iint{\left(\frac{\partial^2\phi\left(\boldsymbol{x}\right)}{\partial x_i\partial x_i}+2G\theta\right)G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA=0} \end{eqnarray} |
上式のG(ξ,x)がGreen関数で、Laplace Equationの場合Green関数は以下です。
| \begin{eqnarray} G\left(\boldsymbol{\xi},\boldsymbol{x}\right)=-\frac{1}{2\pi}{log}_e\left(\frac{r}{r_0}\right) \end{eqnarray} |
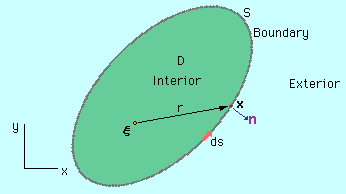
ここにξはSource point、xをObservation point と言います。 これらの2つの点間の距離が上式のrになります。 下図を見て下さい。ξは領域内にxが境界に有る場合を示しています。 今回の場合、2Gθの領域積分があるのでxは領域内にも存在します。 境界要素法では記述を簡略化するために、点を表すときに(x,y)とせずにベクトルxで表します。

有限要素法の場合は、変数の値を計算したい節点がSource pointです。その点を節点Aとすると、節点Aを共有している要素の節点がObservation pointになります。節点Aを共有していない要素はObservation pointになりません。境界要素法では、上のGreen関数で分かる通り、全ての境界要素上の節点がObservation pointになります。 有限要素法と境界要素法の相違点ですが、もう1つあります。境界要素法では部分積分を2回使います。有限要素法では1回でした。境界要素法の詳細についてはサイトを参考にしてください。 まず、1回目の部分積分を上の式に施します。結果は以下です。
\begin{eqnarray} \oint{\frac{\partial\phi\left(\boldsymbol{x}\right)}{\partial x_i}G\left(\boldsymbol{\xi},\boldsymbol{x}\right)n_ids}-\iint{\frac{\partial\phi\left(\boldsymbol{x}\right)}{\partial x_i}\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}dA+2G\theta\iint{G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA=0}} \end{eqnarray}
上の第2項目の領域積分に対し2回目の部分積分を施します。\begin{eqnarray} \oint{\frac{\partial\phi\left(\boldsymbol{x}\right)}{\partial x_i}G\left(\boldsymbol{\xi},\boldsymbol{x}\right)n_ids}-\oint{\phi\left(\boldsymbol{x}\right)\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_ids}+\iint{\phi\left(\boldsymbol{x}\right)\frac{\partial^2G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i\partial x_i}dA+2G\theta\iint{G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA=0}} \end{eqnarray}
ここで気になるのが∂2G(ξ,x)/∂xi∂xiの項 です。実は、ξ=x 以外の点では∂2G(ξ,x)/∂xi∂xi=0です。 確認するために下の極座標系のLaplace EquationにGreen 関数を投入してみます。| \begin{eqnarray} \frac{\partial^2G}{\partial r\partial r}+\frac{1}{r}\frac{\partial G}{\partial r}+\frac{1}{r^2}\frac{\partial^2G}{\partial\theta\partial\theta}=0 \end{eqnarray} |
\begin{eqnarray} \frac{\partial G}{\partial r}=-\frac{1}{2\pi}\left(\frac{1}{r}\right) \end{eqnarray}
そしてGreen 関数の二階微分は以下になります。この様な部分の場合、数学の本に載っている微分式を使うと便利です。\begin{eqnarray} \frac{\partial^2G}{\partial r\partial r}=-\frac{1}{2\pi}\left(-\frac{1}{r^2}\right) \end{eqnarray}
Green 関数はθに関数でないのでθでの二階微分項は以下の様にゼロになります。\begin{eqnarray} \frac{\partial^2G}{\partial\theta\partial\theta}=0 \end{eqnarray}
これらをLaplace Equationに投入すると確かにゼロになります。 では、ξ=xの点ではどうなるのかです。 これを説明するために領域Dを2つに分けます。D-εとεです。
\begin{eqnarray} \iint{\phi\left(\boldsymbol{x}\right)\frac{\partial^2G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i\partial x_i}dA}=\phi\left(\boldsymbol{\xi}\right)\iint{\frac{\partial^2G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i\partial x_i}dA}=\phi\left(\boldsymbol{\xi}\right)\oint{\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_ids} \end{eqnarray}
領域εは円ですのでxi=r, ni=1, ds=εdθになります。loge(r/r0)の微分は1/rです。 再度r0=1と思って下さい。\begin{eqnarray} \phi\left(\boldsymbol{\xi}\right)\oint{\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_ids}=\phi\left(\boldsymbol{\xi}\right)\int_{0}^{2\pi}{\frac{dG\left(\boldsymbol{r}\right)}{dr}\varepsilon}d\theta=\phi\left(\boldsymbol{\xi}\right)2\pi\left(-\frac{1}{2\pi}\frac{1}{\varepsilon}\right)\varepsilon=-\phi\left(\boldsymbol{\xi}\right) \end{eqnarray}
よって部分積分を2回施した式は次の様に記述出来ます。この式のことを境界要素法では境界要素式 またはBoundary Element Equationと呼びます。\begin{eqnarray} \phi\left(\boldsymbol{\xi}\right)=\oint{\frac{\partial\phi\left(\boldsymbol{x}\right)}{\partial x_i}G\left(\boldsymbol{\xi},\boldsymbol{x}\right)n_ids}-\oint{\phi\left(\boldsymbol{x}\right)\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_ids}+2G\theta\iint G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA \end{eqnarray}
ここで境界要素法で使われる変数を定義しておきます。\begin{eqnarray} q_n\left(\boldsymbol{x}\right)=\frac{\partial\phi\left(\boldsymbol{x}\right)}{\partial x_i}n_i \end{eqnarray}
\begin{eqnarray} F\left(\boldsymbol{\xi},\boldsymbol{x}\right)=\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_i \end{eqnarray}
するとBoundary Element Equationは下に示す様にシンプルな形に書けます。\begin{eqnarray} \phi\left(\boldsymbol{\xi}\right)=\oint{q_n\left(\boldsymbol{x}\right)G\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds}-\oint\phi\left(\boldsymbol{x}\right)F\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds+2G\theta\iint G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA \end{eqnarray}
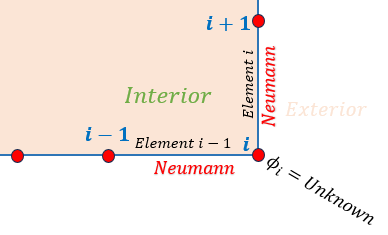
ところでSource pointのξが境界上に有った場合はどうなるか考えてみましょう。上の式はSource pointがInteriorに有る場合でした。下図を参考にして下さい。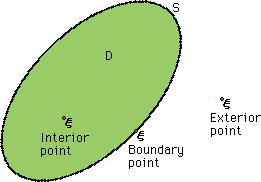
\begin{eqnarray} -1=\oint{\frac{\partial G\left(\boldsymbol{\xi},\boldsymbol{x}\right)}{\partial x_i}n_ids}=\oint F\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds=\int_{0}^{2\pi}{\frac{dG\left(\boldsymbol{r}\right)}{dr}\varepsilon}d\theta \end{eqnarray}
下図に示す様にSource pointが直線またはスムースな境界に有る場合はどうなるか考えてみましょう。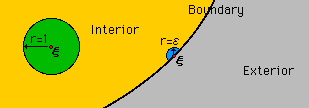
\begin{eqnarray} \oint F\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds=\int_{0}^{\pi}{\frac{dG\left(\boldsymbol{r}\right)}{dr}\varepsilon}d\theta=-0.5 \end{eqnarray}
境界要素法では上の積分項をFree termと呼んでいてC(ξ)で表します。下式の積分記号の前に-符号がついているのに注意して下さい。| \begin{eqnarray} C\left(\boldsymbol{\xi}\right)=-\oint F\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds \end{eqnarray} |
| Source pointの位置 | C(ξ)の値 |
|---|---|
| Interior | 1 |
| Boundary | θ/(2π) |
| Exterior | 0 |
| \begin{eqnarray} C\left(\boldsymbol{\xi}\right)\phi\left(\boldsymbol{\xi}\right)=\oint{q_n\left(\boldsymbol{x}\right)G\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds}-\oint\phi\left(\boldsymbol{x}\right)F\left(\boldsymbol{\xi},\boldsymbol{x}\right)ds+2G\theta\iint G\left(\boldsymbol{\xi},\boldsymbol{x}\right)dA \end{eqnarray} |
| \begin{eqnarray} \left[C\right]\left\{\phi\right\}=\left[G\right]\left\{q_n\right\}-\left[F\right]\left\{\phi\right\}+2G\theta\left\{G\right\} \end{eqnarray} |
■SET4-TORSION-QUARTER.FOR■
とりあえず有限要素法のtorsion4q.forまたはtorsion9q.forで取り上げたのと同じ問題を解いてみましょう。
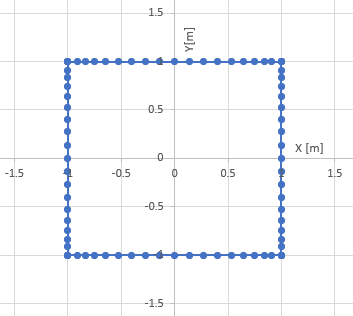
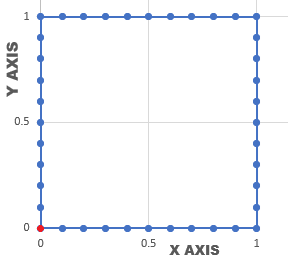
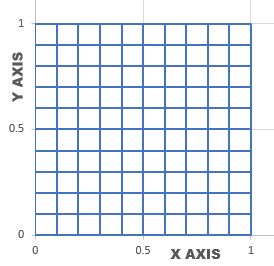
下はNEX=10とNEY=10を用いた境界の分割図です。境界は1次要素で分割してあります。計算領域はfemと同じ1/4モデルです。
| プログラム | 役目 | 入力ファイル | 出力ファイル |
|---|---|---|---|
| SET4-TORSION-QUARTER.FOR | 入力データ作成 | NEX, NEY |
BEM1.DAT
ELEMENT2.OUT ELEMENT4.OUT DOMAIN.DAT PARAM.DAT |
| BEM8LINQ-TORSION.FOR | φの解析 | BEM1.DAT DOMAIN.DAT |
INTERNAL.SOL
SOLUTION4.BIN TORQUEBEM.OUT TRS4DATA.DAT BEM.SOL POSTPROC.DAT |
| GRA4FILE.FOR | φの描画 | BEM1.DAT TRS4DATA.DAT SOLUTION4.BIN | TORSION4.OUT |
■モーメントの計算■
有限要素法のときと同様にここでもモーメントを計算できるようにプログラムを書きました。
モーメントを計算するために下式の領域積分を行う必要があります。
今のプログラムでは2つの方法でモーメントを計算するプログラムを書きました、1つはφの描画の値を使って計算しています。
φの値は領域の要素分割の節点で境界要素式を用い計算されています。
それらの値と形状関数を使ってモーメントを計算します。結果はファイルTORQUEBEM.OUTに入ります。
■角問題(Corner Problems)■
有限要素法では発生しなくて境界要素法で発生する現象が角問題(Corner Problems)です。
理由は、温度、密度、Stress Functionφ等のスカラーを微分するとベクトルになります。
境界でスカラー(φ)を指定するのがDirichlet境界条件で、
スカラーの法線微分(qn=∂φ/∂n)を指定するのがNeumann境界条件です。
境界要素法では、各境界要素においてDirichlet境界条件かNeumann境界条件かを指定しなければなりません。
要素を線積分すると結果は節点に集約されます。
直線状の境界(スムース境界と言う)にこの節点(内角180度)があれば問題ないです。
問題になるのが、Dirichlet境界条件を持つ節点がスムース境界に無い(内角180度以外)ときです。
下図はStress Functionφが既知のスムース境界での節点と要素を表しています。
つまり、節点での内角が180度になっています。
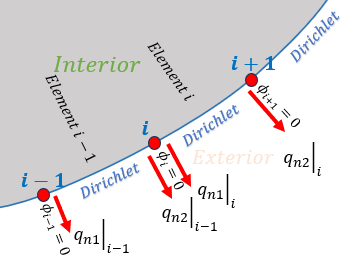
この場合、要素i-1での qn2と要素iでのqn1の方向がそれぞれ同じですよね。 ですので、節点iでStress Functionφの法線方向の微分が1つですので問題無しです。
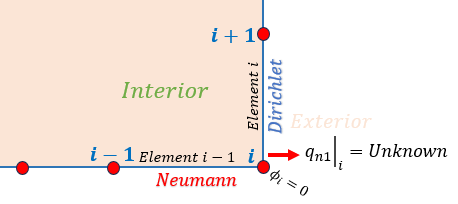
ところが下図の場合はどうでしょう。 節点iの内角が90度です。 節点iでStress Functionφの法線方向の微分qnが2つ存在しますよね。 微分qnが2つ存在するのに解析では節点iのqnとして1つ計算されます。 これが角問題(Corner Problems)です。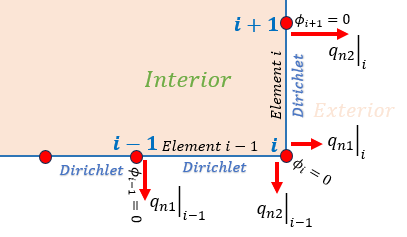
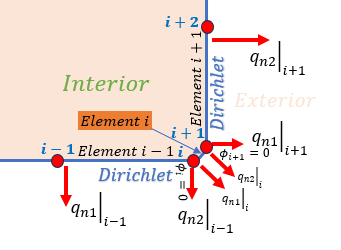
角に2つの節点を置き要素iを設けます。この要素の長さは出来るだけ短くします。 すると問題になっていた角のqnは要素i-1と要素i+1に分けることが出来ます。節点Iの内角は135度になり、90度から少しスムースな境界になっています。 境界要素法では一定要素があります。 要素の中央で境界値を設定します。 この場合、スムースな境界で未知数が計算されますので角問題は発生しません。 BEMサイト では、もう1つ角問題フリーのMIXED要素も紹介してあります。 この要素ではDirichlet境界を節点で指定し、Neumann境界は要素の中央で指定します。
■例題の計算■
角問題についてお話しましたが、角問題の処理を行わず計算を行ってみました。
NEX=NEY=10で境界および領域を要素分割しました。
Shear Modulus G=26538461.5384615[Pa]、θ= 0.0000670055862315403を使いました。
下は同じ条件のFEMの結果をBEMの結果に重ねて表示してあります。

| プログラム | 要素 | 計算方法 | MOMENT [Nm] | MOMENT2 [Nm] |
|---|---|---|---|---|
| torsion4q.for | 1次 | FEM | 3,984.7 | |
| torsion9q.for | 2次 | FEM | 3,999.6 | |
| BEM8LINQ-TORSION-MOMENT.FOR | 1次 | BEM | 3,972.6 | 3,964.6 |
■Warpingの解析■
WarpingについてはTorsion理論のところ示した通り、Neumann境界は文献に示されていましたが、解析に必要なDirichlet境界条件については不明でした。しかし、
Torsionの3次元弾性解析でシャフトが矩形の場合、
断面の4隅のシャフト長手方向の変位がゼロで有ることが判明しました。この事実を使ってWarpingの解析を行ってみます。
まず解かなければ式は下のLaplace Equationでした。
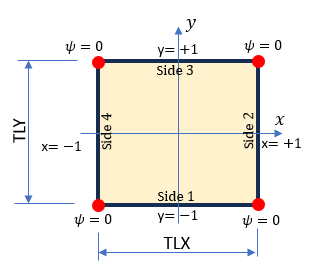
| 項目 | Side 1 | Side 2 | Side 3 | Side 4 |
|---|---|---|---|---|
| dx or dy | dy=0 | dx=0 | dy=0 | dx=0 |
| \begin{eqnarray} \tau_{jz}n_j=0 \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial y}=-x \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial x}=y \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial y}=-x \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial x}=y \end{eqnarray} |
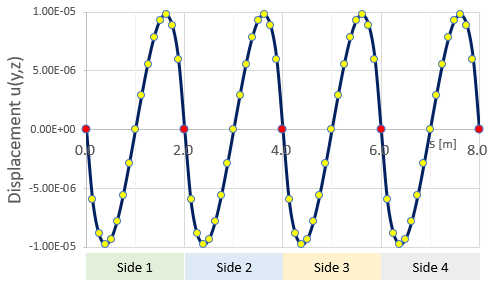
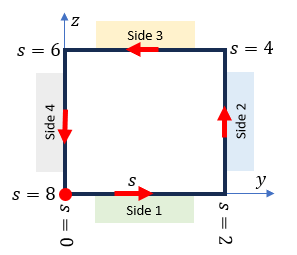
| Side 1 | Side 2 | Side 3 | Side 4 |
|---|---|---|---|
| \begin{eqnarray} \frac{\partial\psi}{\partial n}=-x \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial n}=-y \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial n}=x \end{eqnarray} | \begin{eqnarray} \frac{\partial\psi}{\partial n}=y \end{eqnarray} |
■Warping計算の実行■
境界条件が明白になったので、計算を行ってみます。まず計算に必要なデータを作成する必要があります。ここでは、
SET4-WARPING-FULL.FOR
が作成してくれます。そしてLaplace Equationは
BEM8LINQ-WARPING.FOR
が解いてくれます。以下にこれらのプログラムが入力および出力するファイルを以下に示します。
| プログラム | 入力ファイル | 出力ファイル |
|---|---|---|
| SET4-WARPING-FULL.FOR | なし |
BEM1.DAT
ELEMENT2.OUT |
| BEM8LINQ-WARPING.FOR | BEM1.DAT | SOLUTION.BEM |