■有限要素式■
問題の支配方程式が見つかれば次は重み付け残差法のルールに従って有限要素式を導出すれば解は得られます。
Poisson's Equationを重み付け残差法で展開すると以下になります。重み付け残差法の手続きについては
2次元のFEM
を参考にして下さい。
まずPoisson's Equationに重み関数δφを掛け面積積分しIと置きます。未知数のφが厳密解だとI=0になりますが近似解ですからI≠0です。
| \begin{eqnarray} I=\iint\left(\frac{\partial^2\phi}{\partial x\partial x}+\frac{\partial^2\phi}{\partial y\partial y}+2G\theta\right)\delta\phi dA=\iint\left(\frac{\partial^2\phi}{\partial x_i\partial x_i}+2G\theta\right)\delta\phi dA \end{eqnarray} |
| \begin{eqnarray} I=\oint{q_n\delta\phi ds}-\iint{\frac{\partial\phi}{\partial x_i}\frac{\partial\delta\phi}{\partial x_i}dA+\iint2G\theta\delta\phi dA} \end{eqnarray} |
| \begin{eqnarray} q_n=\frac{\partial\phi}{\partial x_i}n_i \end{eqnarray} |
領域内のφ(x,y)を要素を使って下式にように近似します。 \begin{eqnarray} \phi=\left[N\right]\left\{\phi\right\} \end{eqnarray} \begin{eqnarray} \delta\phi=\left[N\right]\left\{\delta\phi\right\} \end{eqnarray} 境界ではqnとδφは以下で近似します。 \begin{eqnarray} q_n=\left[M\right]\left\{q_n\right\} \end{eqnarray} \begin{eqnarray} \delta\phi=\left[M\right]\left\{\delta\phi\right\} \end{eqnarray}
例えば領域をBilinear要素で近似すると、[N]と[M]は以下の様になります。 \begin{eqnarray} \left[N\right]=\left[\begin{matrix} N_1 & N_2 & N_3 & N_4 \end{matrix}\right] \end{eqnarray} \begin{eqnarray} \left[M\right]=\left[ \begin{matrix} M_ 1& M_2 \end{matrix} \right] \end{eqnarray}
上の近似式を積分式に代入すると以下の有限要素式が得られます。 詳細については、2次元FEMを参考にして下さい。 \begin{eqnarray} I=\left\{\delta\phi\right\}^T\oint{\left[M\right]^T\left[M\right]ds\left\{q_n\right\}}-\left\{\delta\phi\right\}^T\iint{\left[B\right]^T\left[B\right]dA\left\{\phi\right\}+\left\{\delta\phi\right\}^T2G\theta\iint{\left[N\right]^TdA}} \end{eqnarray} 重み付け残差法のルールでは上の式で完成になっています。 しかし2Gθの項が少し理解に苦しむ形になっています。せめて[N]Tでなく{N}になってほしいですよね。 そこで、2Gθは定数ですが関数として以下の様に表します。 \begin{eqnarray} \left\{G\theta\right\}=G\theta\left[N\right]\left\{1\right\} \end{eqnarray} ここに \begin{eqnarray} \left\{1\right\}=\left\{\begin{matrix}\begin{matrix}1\\1\\\end{matrix}\\\begin{matrix}1\\1\\\end{matrix}\\\end{matrix}\right\} \end{eqnarray} すると2G\thetaの項は以下のようになります。 \begin{eqnarray} 2G\theta\iint{\left[N\right]^TdA}=2G\theta\iint{\left[N\right]^T\left[N\right]dA\left\{1\right\}} \end{eqnarray} [N]T[N]{1}を計算すると以下が得られます。 \begin{eqnarray} \left[N\right]^T\left[N\right]\left\{1\right\}=\left\{\begin{matrix}\begin{matrix}N_1\\N_2\\\end{matrix}\\\begin{matrix}N_3\\N_4\\\end{matrix}\\\end{matrix}\right\} \end{eqnarray}
結果的に有限要素式は以下の様に記述できます。 \begin{eqnarray} I=\left\{\delta\phi\right\}^T\oint{\left[M\right]^T\left[M\right]ds\left\{q_n\right\}}-\left\{\delta\phi\right\}^T\iint{\left[B\right]^T\left[B\right]dA\left\{\phi\right\}+\left\{\delta\phi\right\}^T2G\theta\iint\left\{N\right\}dA} \end{eqnarray} ∂I/∂{δφ}T=0を計算すると以下が得られます。 これについても2次元FEMを参考にして下さい。 1次元FinalRemarkも参考にして下さい。 \begin{eqnarray} \oint{\left[M\right]^T\left[M\right]ds\left\{q_n\right\}}-\iint{\left[B\right]^T\left[B\right]dA\left\{\phi\right\}+2G\theta\iint\left\{N\right\}dA}=0 \end{eqnarray} 境界ではDirichlet境界条件のφ=0を与えますのでφの変分δφはゼロになります。そして今回の解析領域として1/4Modelまたは1/2Modelを使いますので対称面のNatural Boundary Conditionを与えます。つまり、qn=0になります。 したがって境界積分の項はφ=0かqn=0になりますのでゼロになってしまいます。 \begin{eqnarray} \iint{\left[B\right]^T\left[B\right]dA\left\{\phi\right\}=2G\theta\iint\left\{N\right\}dA} \end{eqnarray} よって上の式を解けばStress Functionの分布を得ることが出来ます。
■プログラム
torsion4q.for
■
節点が4のIso-parametric要素でPoisson's Equationを解くプログラムを書いてみました。[B]T[B]の積分は本サイトの
2次元Stiffness Matrixを参考にして下さい。
{N}の積分はLaplace Equation関連の問題に無いので新しくサブプログラムを作成することになります。プログラムtorsion4q.forのSUBROUTINE SRCTRMが{N}の積分を行ってくれます。
モーメントの計算は下式に示す通り、Stress functionを面積積分して2倍すれば得られます。
\begin{eqnarray}
M=2\iint\phi dA
\end{eqnarray}
これを行うには、要素毎にStress functionを積分し全ての要素での計算を合計(Σ)すれば得られます。下式を参考にして下さい。
\begin{eqnarray}
M=2\sum\iint\left[N\right]\left\{\phi\right\}dA
\end{eqnarray}
式中の[N]{φ}は要素内のStress functionの分布φ(x,y)を表します。プログラムではSUBROUTINE MOMENTのTORQUEが上式のMに該当します。
| サブプログラム名 | 役目 |
|---|---|
| GSM | 要素毎に[B]T[B]を積分しグローバル“剛性マトリックスRK(I,J)”に足しこみます |
| INPUT | 必要なデータを読み込む |
| 計算結果のStress functionをバイナリー形式でファイルSOLUTION4.BINに書き込む。このファイルがグラフィックプログラムで参照される | |
| PRINTG | ファイルSOLUTION4.FEMに入力データと計算結果を書き込む |
| SRCTRM | 2Gθ∬{N}dAを計算しSOURCE(I)に格納する |
| FORMQ | RK(I,J)= SOURCE(I)の連立方程式に境界条件と境界値を挿入する |
| BANDWID | RK(I,J)のバンド幅を計算する |
| SYSTEM | RK(I,J)= SOURCE(I) の連立方程式を解く |
| GRULE | Gauss-LegendreのSampling points数Nを指定するとξとwを返す |
| ISOPARA | 形状関数[N]が定義されている |
| SHAPEF | 形状関数[N]をξの点で計算する |
| DERIV | 形状関数[N]の微分を計算する |
| MOMENT | M=2∬φdAを計算する |
| ELNDPT | 要素の節点番号と座標値を結び付けている |
| STRESS | τxzとτyzを計算する |
| DERIVX | Stress functionの微分を計算する |
| DAREA | 要素の面積を計算する |
■データ作成プログラムsettrs4.for■
入力データを手で作成するのは大変ですので、プログラムを使います。
プログラムtorsion4q.forに必要な全てのデータは少ないパラメータを指定するだけで要素から境界条件までを作成しファイルに書き込みます。
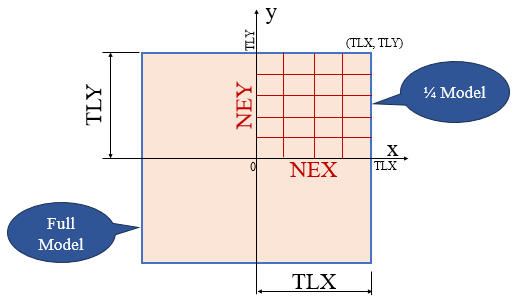
まず下図を見て下さい。
これは全計算領域の1/4です。ここでは1/4モデルと言うことにします。

図では四角形が全体モデル(Full Model)ですが、Iso-parametric要素を使っていますので、円形のモデルでも計算してくれます。 図に出てくる変数の意味は以下になります。
| 変数 | 意味 |
|---|---|
| TLX | 1/4 Modelのx方向の長さ |
| TLY | 1/4 Modelのy方向の長さ |
| NEX | x方向の要素の分割数(図では4) |
| NEY | y方向の要素の分割数(図では5) |
図ではx方向の要素の分割数が4で、y方向の要素の分割数が5になっています。 プログラムではNEXとNEYの入力を要求してきます。 プログラムでは計算を行う上で以下の数値が使われています。
| TLX | TLY | Shear Modulus [Pa] | Rate of Twist(θ) |
|---|---|---|---|
| 1 | 1 | 26538461.5384615 | 0.0000670055862315403 |
■settrs4.forの実行より作成されるファイル■
まずsettrs4.forをNEX=10とNEY=10で実行します。すると以下のファイルが作成されます。
| 出力ファイル名 | 中身 |
|---|---|
| TRS4DATA.DAT | ねじれ解析のPoisson’s Equationを解くためのプログラムtorsion4q.for用のデータが入っている |
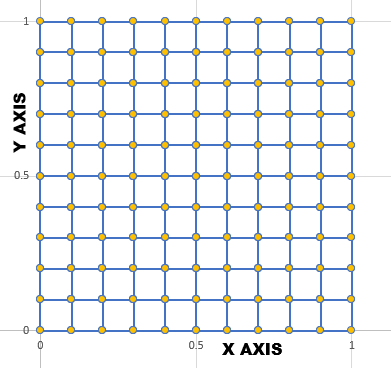
| ELEMENT4.OUT | 要素分割図を描くためのデータです。エクセルにドラッグアンドドロップしてデータタグの区切り位置で“コンマや…”を選択し、区切り文字のスペースを選択すると、B列とC列に数値が入ります。B列をx軸、C列をy軸の散布図として図が描けます。下図がそうです |
■解析プログラムtorsion4q.forの実行■
続いてtorsion4q.forを実行します。以下のファイルが出力されます。
| 出力ファイル名 | 中身 |
|---|---|
| SOLUTION4.FEM | テキストファイルですので、メモ帳で中身を見られます。要素情報と節点の座標、計算領域の面積、境界条件とその値、Stress Function (φ)の節点での値、モーメント値(TORQUE)、節点でのせん断応力τzxとτzyが入っています。 |
| SOLUTION4.BIN | Stress Function (φ)、τzxとτzyの等高線をプログラムGRA4FILE.FORで描くためのデータです。バイナリーファイルです。 |
| 要素 | 1/4モデルのM [Nm] | フルモデル換算のM [Nm] |
|---|---|---|
| 4-Noded | 995.1 | 3980 |
| 9-Noded | 998.8 | 3995 |
■描画プログラムGRA4FILE.FORの実行■
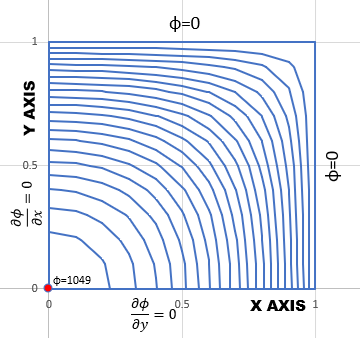
Stress Function (φ)の等高線を描くことが出来ます。このプログラムを実行すると以下のファイルを出力します。
| 出力ファイル名 | 中身 |
|---|---|
| TORSION4.OUT | Stress Function (φ)の等高線を描くためのデータです。エクセルにドラッグアンドドロップします。後は要素分割図と同じ手順です。 |
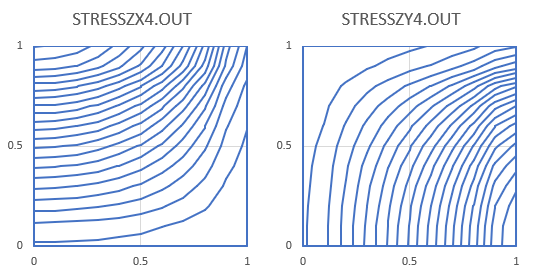
| STRESSZX4.OUT | τzxの等高線を描くためのデータです。エクセルにドラッグアンドドロップします。後は要素分割図と同じ手順です。 |
| STRESSZY4.OUT | τzyの等高線を描くためのデータです。エクセルにドラッグアンドドロップします。後は要素分割図と同じ手順です。 |
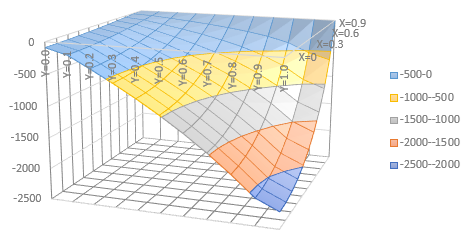
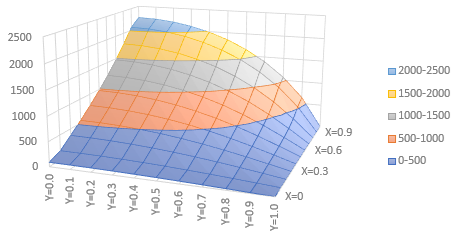
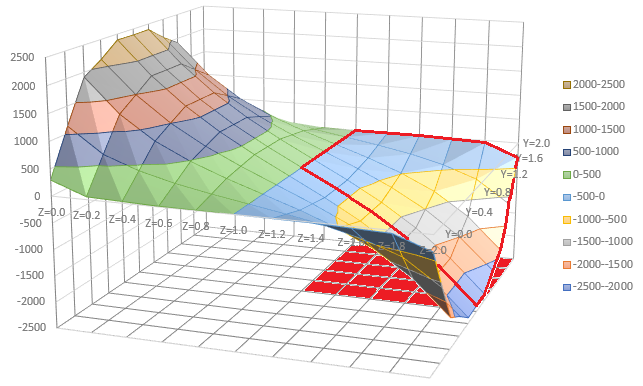
■断面が円形の場合■
これまではシャフトの断面が2m×2mの矩形(1/4Modelでは1m×1m)でしたが、ここでは断面が円形のStress Functionを計算してみます。断面の大きさですが、Saint Venant theoryに従い矩形のモーメントと円形のモーメントが同じになるように決めました。
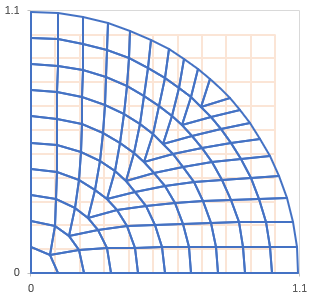
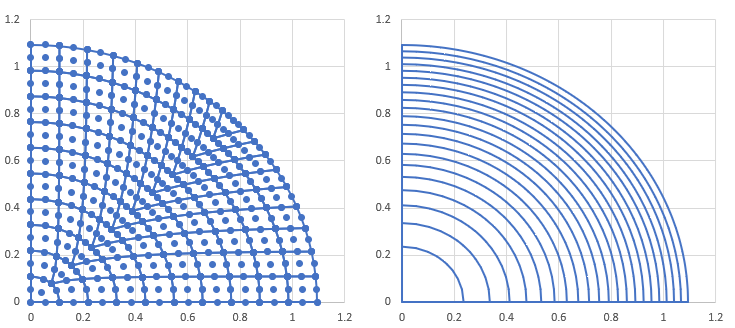
矩形の断面積は2m×2m=4m2のとき、円形の断面積はA=3.7647m2でした。この場合の半径が下図のように1.09469mになります。
入力データは、settrs4-one-fourth-circle.for
で作成できます。薄い色で描かれている要素分割は矩形断面の2m×2mです。
■9-Noded解析プログラムtorsion9q.for■
一通りTorsion問題は解けました。ここでは、解析精度を向上させるために、2次要素を使って計算を行ってみます。要素は、下図に示す節点が9つあるIso-parametric です。
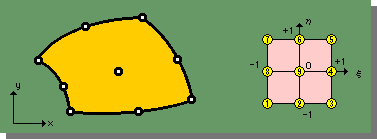
この要素を使ってTLX=1, TLY=1, NEX=10, NEY=10で分割すると以下のようになります。この要素は要素内に節点が1つ有るのが特徴です。要素の境界上には節点が3つありますので2次の要素ということになります。
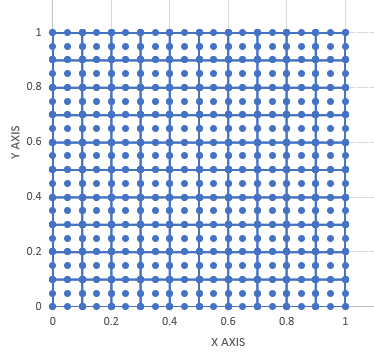
入力データ TRS9DATA.DAT は、settrs9.forで作成できます。 torsion9q.forによる計算結果は、SOLUTION9.FEMに入ります。
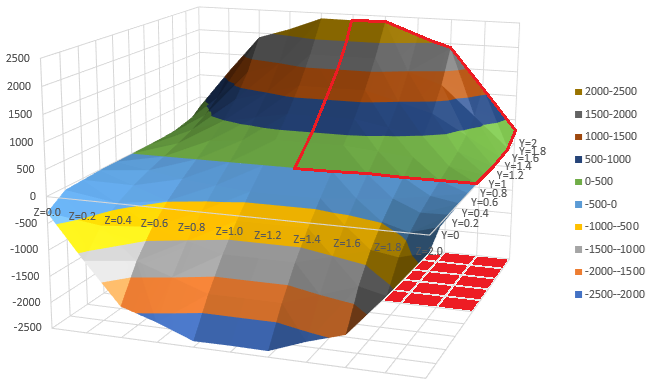
Stress Function、τzx、τzyのエクセル用の描画データは GRA9FILE.FOR で作成できます。下はGRA9FILE.FORが出力したデータを使って描いたStress Functionです。4-Noded要素の計算結果より線がスムースですね。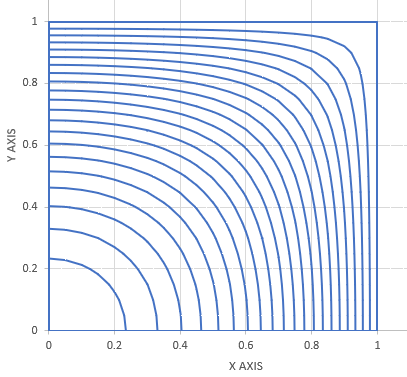
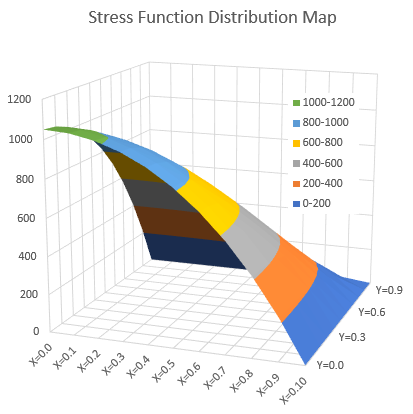
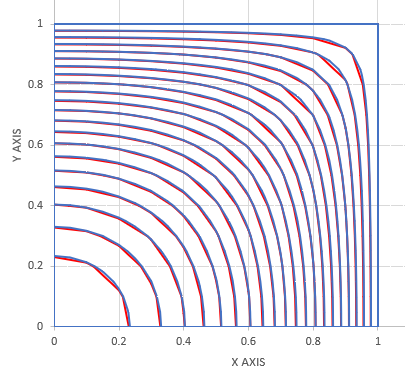
これで有限要素法の話は終わりにしておきます。