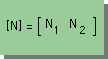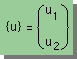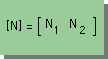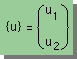One Dimensional Finite Element Method
Final Remark-2
■近似式と重み関数のマトリックス表示■
有限要素法で微分方程式を解析するためには有限要素式をマトリックスとベクトルの形で表現す必要が有ります。
つまり近似式と重み関数をマトリックス形式で書き表す必要があるということです。
では早速近似式をマトリックス記述法で書いてみましょう。
次の様になります。
|
|
ここに、 |
 |
|
 |
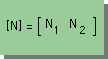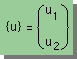同様に新しい重み関数も次の様に書けます。
|
|
ここに、 |
 |
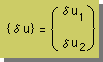解析したい微分方程式を、これまで使ってきたHelmholtz Equation
∇2u+α2u=0
とするとResidualは下図に示す様に書くということは以前述べましたね。
\begin{eqnarray}
\frac{\partial^2u}{\partial x \partial x} + \alpha^2u=R\left(u\right)
\end{eqnarray}
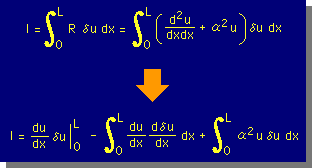
すると積分式(I)は新しい重み関数を用いると、どのように展開できるでしょうか。
貴方も考えてみて下さい。
結果は下図の様になります。
貴方もそう成るということを確認して下さい。
それほど難しくないですから。
このページに記載してある内容は有限要素法の勉強の中で最も重要な事柄ですのでしっかりと勉強して下さい。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method