helmholtz Equation

One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-5

ちょっと脱線しましたね。話しを本題に戻しましょう。先程、ΣM_z=0より式を導きましたよね。この式を円の微分方程式に代入します。すると、次に示すビームの微分方程式が得られます。円の微分方程式の1/Rがｙの関数になっているのに注意して下さい。つまり、両端にピュア-なモーメントが作用していない場合、ビームは円弧にならないことになります。

上の式は、ちょと複雑すぎますよね。それに、非線形な微分方程式になっています。そこで、仮定として、ビームの変形が小さいと考えます。すると、(dY/dx)²≒0としても、結果に大きな誤差は招かないと思われます。

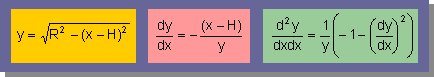
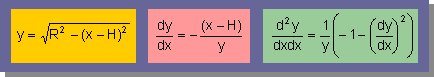
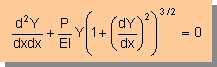
■支配方程式■
そこで、上式の(dY/dx)²をゼロとおくと、ここで取り扱っているバックリング問題の微分方程式が出来上がります。このような微分方程式を支配方程式(Governing Equation)といい、下の様な式になります。また、下の式は、線形で Helmholtz Equationと呼ばれています。

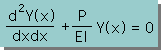
上の式が、正しいかどうか、チェックしてみましょう。力(P)が大きくなると、2階微分項が負の大き数値になります。つまり、ビームが大きな山形になることを意味しています。また、EIが小さくても同様な現象が起きることになります。この微分方程式は、簡単な式ですが、十分技術問題の解決に役立ちそうですね。
有限要素法の話しを進めるために、上の微分方程式を次のように表わすことにします。

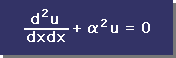
■境界条件■
微分方程式の解を得るためには、境界条件が必要です。つまり、微分方程式に境界条件を与えることにより、 1つの問題に焦点を当てた解が得られることになります。境界条件の種類には、下表に示すように、 3つが考えられます。

呼び名	愛称	式	意味
Dirichlet BC	1st Kind B. C.	u(0)=c, u(L)=d	未知数が境界で固定される
Neumann BC	2nd Kind B. C.	du(0)/dx=e, du(L)/dx=f	未知数の勾配が境界で固定される
Robin C* Cauchy BC#	Third Kind BC or Mix kind BC	u(0)+du(0)/dx=g, u(L)+du(L)/dx=h	(未知数+未知数の勾配)が境界で固定される
BC= Boundary Condition, 1st=First, 2nd=Second, C=Condition *光・波動のための有限要素法の基礎、小柴正則著、森北出版（1990), #Bear, Jacob

ここで紹介している微分方程式は、2階微分項が最高微分項ですから、境界条件の数は2つ必要です。境界条件の種類や形については、各セックションで詳しくふれます。

次に進む前に、左をクリックして問題を解いて下さい。

BACK	NEXT