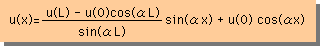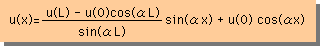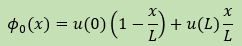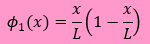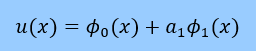One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-6
■厳密解■
バックリング問題の支配方程式であるHelmholtz Equationを、両端Dirichlet境界条件で解くと、次のようになります。
実際の厳密解は、複素数(complex number)になります。
実数部が下式で虚部にはゼロが入ります。
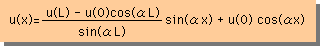
上の式が正しいかどうか、貴方も確かめてみて下さいね。
Program exact.forも参考にして下さい。
このプログラムは、コンソールからデータを入力します。
計算結果は、ファイルEXACT.DATに入ります。
計算の一例をここに示します。
■近似式■
次に 変数αが限りなくゼロに近いときの 上のu(x)はどうなるか考えてみよう。
貴方もやってみて下さいね。
結果的に次の様になります。
これは 支配方程式のαをゼロとしたときと同じになります。
つまり 線形の式です。
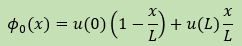
仮に この式をHelmholtz Equationの解と考えると 上の式は、自由度がゼロの解といえます。
つまり、αの変化に対応出来ないからです。
では αの変化に対応出来る最低限の近似式は、どの様なものでしょう。
ここからは、有限要素法のキーになる部分ですので注意深く観察して下さい。
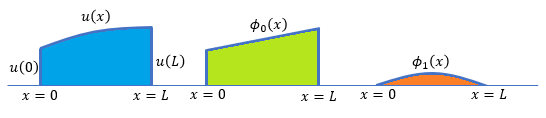
まず下の図を見て下さい。
左が求めようとしている近似解で、真ん中がα=0の解で、そして右がαの変化を吸収してくれる関数です。
この関数の値は両端でゼロになっていることに注意して下さい。
 上図の右のグラフは下の式で書けそうな気がします。
上図の右のグラフは下の式で書けそうな気がします。
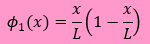 すると、近似式は次のように書けます。
この様に未知数(a1)が1つ存在することを自由度が1の近似式といいます。
ここで注意したいことは、両境界とも Dirichlet 境界条件(u(0) and u(L))であるということです。
つまり、この近似式は両端がDirichlet 境界条件のときのみ有効であると言うことです。
Neumann境界については後で勉強します。
すると、近似式は次のように書けます。
この様に未知数(a1)が1つ存在することを自由度が1の近似式といいます。
ここで注意したいことは、両境界とも Dirichlet 境界条件(u(0) and u(L))であるということです。
つまり、この近似式は両端がDirichlet 境界条件のときのみ有効であると言うことです。
Neumann境界については後で勉強します。
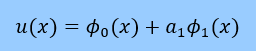 上の近似式についてちょっとコメントしておきます。
上の近似式についてちょっとコメントしておきます。
| φ0の目的 |
φ1の目的 |
| 境界値のみで構成されている |
α2のみに関係し近似解の精度を司る |
さて、次はどのようにして a1 を求めるかです。
誰でも考え付くのが、この近似式をHelmholtz Equationに直接代入して、a1を求める方法ですかね。
確かに、なんらかの解は得られますが、解の信頼生が不明です。
また、近似式の中に、a1とa2の2つがある場合の計算ができません。
そこで有限要素法の登場になります。
次のセックションでは、a1を求める1つの方法である
Weighted Residual Method を紹介します。
その前に、ここで勉強したことをまとめておきました。NEXTをクリックして下さい。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method