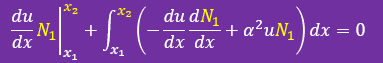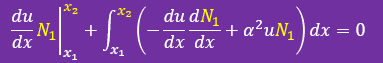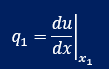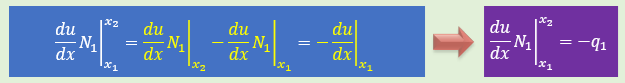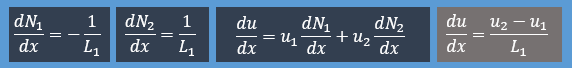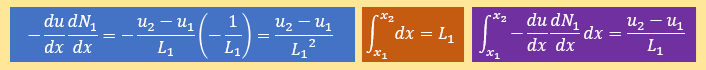One Dimensional Finite Element Method
Linear Element-6
積分式の重み関数φ1(x)をN1(x)で置き換えると次の様になります。
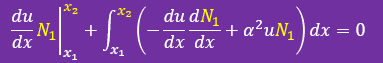 まず上式の境界積分項ですがN1(x2)=0 で N1(x1)=1 ですから
(du/dx)N1はxがx1でのdu/dxになります。ここでは便宜上下式のように定義します。
言葉で言うとx=x1でのdu/dxをq1とする。
まず上式の境界積分項ですがN1(x2)=0 で N1(x1)=1 ですから
(du/dx)N1はxがx1でのdu/dxになります。ここでは便宜上下式のように定義します。
言葉で言うとx=x1でのdu/dxをq1とする。
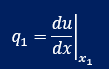 上式の定義は今後Neumann型境界条件として扱われます。ここではBeamの勾配が指定できるということにしておきます。
よって境界積分は次の様になる。
上式の定義は今後Neumann型境界条件として扱われます。ここではBeamの勾配が指定できるということにしておきます。
よって境界積分は次の様になる。
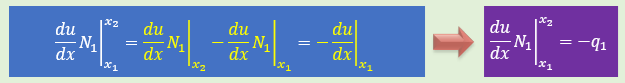 次の領域積分では形状関数と未知数の微分が必要になります。
それらを計算すると次の様になります。
またu(x)=u1N1(x)+u2N2(x)だということをお忘れなく。
次の領域積分では形状関数と未知数の微分が必要になります。
それらを計算すると次の様になります。
またu(x)=u1N1(x)+u2N2(x)だということをお忘れなく。
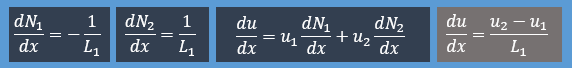 ここにL1は要素1の長さを意味します。したがって微分項の領域積分結果は下図の様にります。
ここにL1は要素1の長さを意味します。したがって微分項の領域積分結果は下図の様にります。
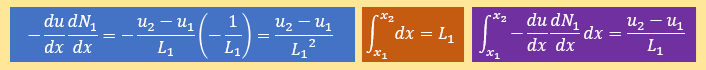 そして、α2の項の積分にある uN1は要素1での近似式より次のように書けます。
そして、α2の項の積分にある uN1は要素1での近似式より次のように書けます。
 u(x)N1(x)の積分で注意してもらいたい事が1つ有ります。一般にこの項のことを微分方程式では生成項(Source Term)と言い稀にこの項に独立変数(independent Variable)が含まれていることがあります。1次元Helmholtz Equstion の場合、独立変数は x ですがここで紹介しているHelmholtz Equstionには独立変数は有りません。
u(x)N1(x)の積分で注意してもらいたい事が1つ有ります。一般にこの項のことを微分方程式では生成項(Source Term)と言い稀にこの項に独立変数(independent Variable)が含まれていることがあります。1次元Helmholtz Equstion の場合、独立変数は x ですがここで紹介しているHelmholtz Equstionには独立変数は有りません。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method