One Dimensional Finite Element Method
Final Remark-11
■重み関数δu(x) の意味■
ここからは、説明が少し抽象的になりますので話しを聞きたくない人は次の
2次要素へ御進み下さい。
ここで紹介した重み関数δu(x) は近似式と同様な形をしているということに注目して下さい。
このことを利用して次の仮説を立ててみたいと思います。
| δu(x) を厳密解ue と近似解u(x)との差であると考える。 |
|---|
| ue(x) = u(x) + δu(x) |
|---|
| つまり、δu(x)を解析誤差と考える。 |
|---|
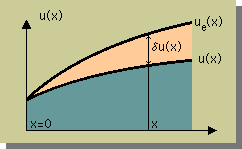 上の式をグラフにすると、右図の様になります。
図によると x=0 で Dirichlet境界条件が与えられています。
Dirichlet条件が与えられている境界では厳密解と近似解が同じになるため誤差はゼロになります。
したがって at x=0 では δu(x)=0 になります。 上の式をグラフにすると、右図の様になります。
図によると x=0 で Dirichlet境界条件が与えられています。
Dirichlet条件が与えられている境界では厳密解と近似解が同じになるため誤差はゼロになります。
したがって at x=0 では δu(x)=0 になります。
このことは連立方程式の
Dirichlet境界条件を組み込む手順に反映されています。
つまり”Dirichlet境界条件が組み込まれる連立方程式の行(row)に存在している全ての値をゼロにする”でした。
結果的にDirichlet境界条件の節点につて有限要素式を立てる必要はないことになります。
何故かと言うと、誤差がゼロ、またはδu(x)=0 だからです。
|
Neumann型境界上で δu(x)はどんな値をもってるか調べてみましょう。
例として x=L の点で du/dx=0 を考慮します。
WRM-対称条件で説明しましたが形状関数の形の違いや要素分割数の違いで u(L) は変化します。
つまり誤差≠0 ですから δu(L)≠0 となります。
■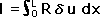 とδu(x)の関係■
とδu(x)の関係■
δu(x)を誤差として仮定したので、積分 I は最低δu(x)の二乗になるはずである。
何故なら残差 R も間接的にδu(x)の関数であるからである。
と言っても、R(u(x))=f(δu(x))については、かなり無理があります。
”この仮説は気に食わない”とおっしゃる方は
次の2次要素へ御進み下さい。
次回貴方がこのsiteへ訪れるまでには、もっと納得できる仮説を用意しておきます。
実際、R(u(x))=誤差の集合 には違いないのですが、数式展開の中では、R(u(x))=f(δu(x))となっていません。
しかし、δu(x)のδuiは数式展開において δui≠0 としているだけで、その他になにも制限を受けていません。
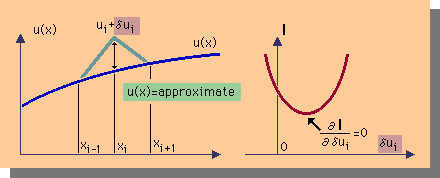
とりあえず話しを進めましょう。上の議論を頭に入れて、下の左の図を見て下さい。
縦軸がu(x)で横軸がxです。そして、図中のu(x)は計算されたばかりの近似解です。
その近似解のuiだけにδuiを加算します。
そして δuiを変化し積分 I を計算出来たとします。
すると結果は下の右の図の様になるはずです。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
 上の式をグラフにすると、右図の様になります。
図によると x=0 で Dirichlet境界条件が与えられています。
Dirichlet条件が与えられている境界では厳密解と近似解が同じになるため誤差はゼロになります。
したがって at x=0 では δu(x)=0 になります。
上の式をグラフにすると、右図の様になります。
図によると x=0 で Dirichlet境界条件が与えられています。
Dirichlet条件が与えられている境界では厳密解と近似解が同じになるため誤差はゼロになります。
したがって at x=0 では δu(x)=0 になります。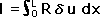 とδu(x)の関係■
とδu(x)の関係■