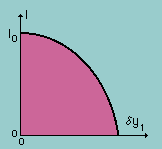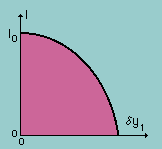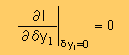ここで、δy(x)は、次の様に定義してみましょう。

そして、δy(x)またはδy₁は非常に小さな値を持つ関数ということにします。つまり、δy(x)² nealy equal to 0 になるということです。φ₁(x)は、WRMの例題の、ξ(1-ξ)を使います。ξ=x/L でしたね。 後で詳しく説明しますが、実は、このδy(x) が有限要素法の重み関数なのです。また、δy(x)のことを、厳密解からの変分と言います。

領域の両端が Dirichlet 境界ですから、境界では、近似解と厳密解のy(x)が同じになります。つまり、次の様です。

上の条件から、δy(0)=δy(L)=0 または φ₁(0)=φ₁(L)=0 になりますね。上の図(前のページ)も参考にして下さい。つまり、平たく言うとDirichlet型境界では、誤差も変分もゼロと言うことですね。

次に、δy₁ を変化させた時に、積分式の値(I)が、どの様になるかチェックしてみましょう。多分、皆様も想像つくと思いますが、下図の様になります。後ほど、例題を使って I を計算してみます。

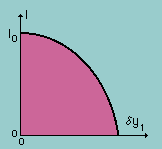δy₁ がゼロの位置で、I₀ になっていることに注意して下さいね。つまり、δy₁ を小さくして行くと、上の図から I は I₀ に近づくことは明らかですね。実際の問題では、 I₀ の値は分かっていませんし、δy₁ も存在しません。1つ明らかなことは、 I₀ がδy₁=0 で極値(最大または最小)になっていると仮定すると、上の図から、次の条件式が考えられます。つまり、関数の凸になっている点や凹んでいる点を探す条件式ですよね。

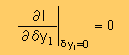と、まー、こんな風にして話を先へ進めることはできますが、このままでは、話がだんだん難しくなり、皆様に読んでもらえない Homepage になってしまいます。そこで、ここでは、他の本にない方法で、話を進めることにしましょう。